题目内容
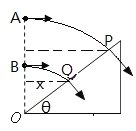
【题目】如图所示,O为斜面的底端,在O点正上方的A、B两点分别以初速度vA、vB正对斜面抛出两个小球,结果两个小球都垂直击中斜面,击中的位置分别为P、Q(图中未标出)。OB=AB,空气阻力忽略不计,则( )
A. OP=![]() OQ B. OP=4OQ C. vA=
OQ B. OP=4OQ C. vA=![]() vB D. vA=vB
vB D. vA=vB
【答案】C
【解析】
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据速度的方向,通过平行四边形定则求出小球打在斜面上时的速度大小以及竖直方向上的分速度,从而求出飞行的时间。
设任一小球初速度为![]() ,抛出点的高度为
,抛出点的高度为![]() ,运动时间为
,运动时间为![]() ,斜面的倾角为
,斜面的倾角为![]()
根据题意,小球垂直击中斜面,速度与斜面垂直,由速度分解可知:![]()
又![]() ,可得:
,可得:![]()
根据几何关系得:![]()
根据2OA=OB,则得:![]()
根据几何关系可得:![]()
所以![]()
故本题选C。

练习册系列答案
相关题目