题目内容
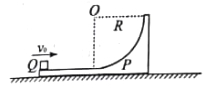
【题目】如图所示，ABC为一固定在竖直平面内的光滑轨道，BC段水平，AB段与BC段平滑连接。质量为m1的小球从高h处由静止开始沿轨道下滑，与静止在轨道BC段上质量为m2的小球发生碰撞，碰撞前后两球的运动方向处于同一水平线上，且在碰撞过程中无机械能损失。
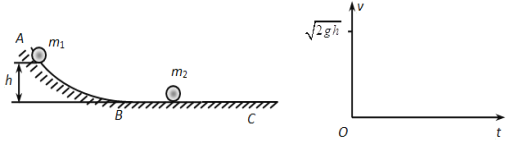
①求碰撞后小球的m2速度大小v2；
②在两球碰撞过程中，把从两球开始接触到形变达到最大值，称为压缩阶段。在图中的坐标系中，定性画出在压缩阶段两小球的速度随时间变化的图像；并求出两小球形变最大时，系统的弹性势能Ep。
【答案】（1）
（2）图见解析；
【解析】
①m1从初始高度h由静止下滑，到达水平面时的速度为 v0
根据动能定理可得：
解得：
m1球和m2球碰撞过程中，动量守恒、机械能守恒，则有：
解得：
② 压缩阶段m1做加速度增大的减速运动，m2球做加速度增大的加速运动，v-t图像如图所示
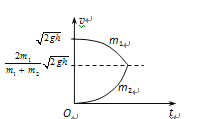
两球碰撞过程中，形变最大时两球具有相同的速度，根据动量守恒有：
解得：
最大弹性势能：
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
