题目内容
10. 如图,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g.
如图,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g.(1)求滑块从静止释放到与弹簧上端接触前,运动的加速度是多大?
(2)在沿斜面向下运动的过程中,若已知滑块运动最大速度大小为vm,求此时弹簧的压缩量x是多少?
(3)求滑块从静止释放到速度达到最大vm过程中,滑块克服弹簧弹力所做的功W.
分析 (1)滑块从静止释放到与弹簧上端接触前,由牛顿第二定律求出加速度.
(2)滑块所受合力为零时速度最大,由平衡条件求出滑块速度最大时弹簧的压缩量.
(3)根据动能定理求滑块克服弹簧弹力所做的功W.
解答 解:(1)滑块从静止释放到与弹簧上端接触前,对滑块,由牛顿第二定律得滑块的加速度为:
a=$\frac{qE+mgsinθ}{m}$=$\frac{qE}{m}$+gsinθ
(2)当滑块速度最大时,滑块受到的合力为零,则qE+mgsinθ=kx,
解得:x=$\frac{qE+mgsinθ}{k}$
(3)从滑块开始运动到速度最大过程中,由动能定理得:
(qE+mgsinθ)(x+s0)-W=$\frac{1}{2}m{v}_{m}^{2}$,
解得:滑块克服弹簧弹力所做的功为:
W=(qE+mgsinθ)(x+s0)-$\frac{1}{2}m{v}_{m}^{2}$=(qE+mgsinθ)($\frac{qE+mgsinθ}{k}$+s0)-$\frac{1}{2}m{v}_{m}^{2}$.
答:(1)滑块从静止释放到与弹簧上端接触前,运动的加速度是$\frac{qE}{m}$+gsinθ.
(2)此时弹簧的压缩量x是$\frac{qE+mgsinθ}{k}$.
(3)滑块克服弹簧弹力所做的功W为(qE+mgsinθ)($\frac{qE+mgsinθ}{k}$+s0)-$\frac{1}{2}m{v}_{m}^{2}$.
点评 本题考查了求滑块的运动时间、弹簧的弹性势能、滑块的路程,分析清楚滑块运动过程是正确解题的关键,应用牛顿第二定律、平衡条件、运动学公式、动能定理、能量守恒定律即可正确解题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
1.以下是有关近代物理内容的若干叙述,其中正确的是( )
| A. | 原子核发生一次β衰变,该原子外层就失去一个电子 | |
| B. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,但原子的能量增大 | |
| C. | 一束光照射到某种金属上不能发生光电效应,可能是因为这束光的光强太小 | |
| D. | 比结合能越大,原子核中核子结合得越牢固,原子核越稳定 | |
| E. | 太阳辐射的能量主要来自太阳内部的聚变反应 |
18. 如图所示,在倾角为30°的粗糙斜面上有一重为G的物体,若用与斜面底边平行的恒力F=$\frac{G}{2}$推它,恰好能使它做匀速直线运动.物体与斜面之间的动摩擦因数为( )
如图所示,在倾角为30°的粗糙斜面上有一重为G的物体,若用与斜面底边平行的恒力F=$\frac{G}{2}$推它,恰好能使它做匀速直线运动.物体与斜面之间的动摩擦因数为( )
 如图所示,在倾角为30°的粗糙斜面上有一重为G的物体,若用与斜面底边平行的恒力F=$\frac{G}{2}$推它,恰好能使它做匀速直线运动.物体与斜面之间的动摩擦因数为( )
如图所示,在倾角为30°的粗糙斜面上有一重为G的物体,若用与斜面底边平行的恒力F=$\frac{G}{2}$推它,恰好能使它做匀速直线运动.物体与斜面之间的动摩擦因数为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{6}$ |
5.“嫦娥二号”进入环月轨道后,分别在距月球表面最远100km,最近15km高度的轨道上做圆周运动,此高度远小于月球的半径,设“嫦娥二号”绕月与月绕地的转动方向同向.已知地球的质量为月球质量的k倍,月球绕地球运行的轨道半径为月球的半径的n倍,月球绕地球运行的周期为T.若某时刻“嫦娥二号”距地球最远,经△t时间“嫦娥二号”距地球最近,则△t不可能为( )
| A. | $\frac{T}{2(1-\sqrt{\frac{k}{{n}^{3}}})}$ | B. | $\frac{T}{2(\sqrt{\frac{{n}^{3}}{k}}-1)}$ | C. | $\frac{T}{2(\sqrt{\frac{k}{{n}^{3}}}-1)}$ | D. | $\frac{T}{2(1-\sqrt{\frac{{n}^{3}}{k}})}$ |
19. 三个分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同速度V0垂直电场线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如图所示,下面判断正确的是( )
三个分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同速度V0垂直电场线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如图所示,下面判断正确的是( )
 三个分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同速度V0垂直电场线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如图所示,下面判断正确的是( )
三个分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同速度V0垂直电场线方向射入匀强电场,分别落在带正电荷的下板上的a、b、c三点,如图所示,下面判断正确的是( )| A. | 落在a点的颗粒带正电、C点的带负电、b点的不带电 | |
| B. | 落在a、b、c点颗粒在电场中的加速度大小的关系是a>b>c | |
| C. | 三个颗粒在电场中的运动时间关系是a>b>c | |
| D. | 电场力对落在b点的颗粒不做功 |
20.两个形状相同的绝缘小球,它们带电量分别为+Q与-5Q,两球相距一定的距离,今把它们相接触后置于原处,则它们之间相互作用力与原来相比将( )
| A. | 变小 | B. | 变大 | ||
| C. | 不变 | D. | 以上三种情况都有可能 |
 如图所示,车间内的天车(有的地区交行车)将一重104N的物体沿着与水平方向成30°角的方向匀速吊起,使物体向斜上方移动了x1=6m,求:
如图所示,车间内的天车(有的地区交行车)将一重104N的物体沿着与水平方向成30°角的方向匀速吊起,使物体向斜上方移动了x1=6m,求: 如图所示,一半径为R的绝缘圆形轨道竖直放置,圆形轨道的最低点与一水平轨道相连,轨道都是光滑的,轨道所在的空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m的带正电的小球,为使小球刚好能在竖直面内完成圆周运动,求释放点A距圆轨道最低点B的距离s.已知小球受的电场力等于小球重力的$\frac{3}{4}$.
如图所示,一半径为R的绝缘圆形轨道竖直放置,圆形轨道的最低点与一水平轨道相连,轨道都是光滑的,轨道所在的空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m的带正电的小球,为使小球刚好能在竖直面内完成圆周运动,求释放点A距圆轨道最低点B的距离s.已知小球受的电场力等于小球重力的$\frac{3}{4}$.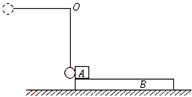 质量为mB=6kg的木板B静止于光滑水平面上,物块A质量为mA=1kg,停在B的左端.质量为m=1kg的小球用长为l=0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞,碰撞时间极短,且无机械能损失.物块与小球可视为质点,不计空气阻力.已知A、B间的动摩擦因数μ=0.1,A离开B时的速度是B的2倍,g取10m/s2.求木板的长度d?
质量为mB=6kg的木板B静止于光滑水平面上,物块A质量为mA=1kg,停在B的左端.质量为m=1kg的小球用长为l=0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞,碰撞时间极短,且无机械能损失.物块与小球可视为质点,不计空气阻力.已知A、B间的动摩擦因数μ=0.1,A离开B时的速度是B的2倍,g取10m/s2.求木板的长度d?