题目内容
5.“嫦娥二号”进入环月轨道后,分别在距月球表面最远100km,最近15km高度的轨道上做圆周运动,此高度远小于月球的半径,设“嫦娥二号”绕月与月绕地的转动方向同向.已知地球的质量为月球质量的k倍,月球绕地球运行的轨道半径为月球的半径的n倍,月球绕地球运行的周期为T.若某时刻“嫦娥二号”距地球最远,经△t时间“嫦娥二号”距地球最近,则△t不可能为( )| A. | $\frac{T}{2(1-\sqrt{\frac{k}{{n}^{3}}})}$ | B. | $\frac{T}{2(\sqrt{\frac{{n}^{3}}{k}}-1)}$ | C. | $\frac{T}{2(\sqrt{\frac{k}{{n}^{3}}}-1)}$ | D. | $\frac{T}{2(1-\sqrt{\frac{{n}^{3}}{k}})}$ |
分析 根据万有引力提供向心力,列出等式,解出“嫦娥二号”绕月球运动的周期与月球绕地球运动的周期的关系,进一步计算出月球的角速度ω和“嫦娥二号”的角速度ω′.
由于“嫦娥二号”绕月与月绕地的转动方向同向,所以有π=(ω′-ω)•△t,代入数据化简,可得到△t的值.
解答 解:对于月球绕地球运动,根据万有引力提供向心力$G\frac{{M}_{地}{M}_{月}}{(n{R}_{月})^{2}}={M}_{月}\frac{4{π}^{2}}{{T}^{2}}(n{R}_{月})$,即${GM}_{地}=\frac{4{π}^{2}{n}^{3}{{R}_{月}}^{3}}{{T}^{2}}$
又因为已知地球的质量为月球质量的k倍,所以${GkM}_{月}=\frac{4{π}^{2}{n}^{3}{{R}_{月}}^{3}}{{T}^{2}}$
对于“嫦娥二号”绕月球运动,$G\frac{{M}_{月}m}{{{R}_{月}}^{2}}=\frac{4{π}^{2}}{{T′}^{2}}{R}_{月}$,即${GM}_{月}=\frac{4{π}^{2}{{R}_{月}}^{3}}{{T′}^{2}}$
所以T′=$\sqrt{\frac{k}{{n}^{3}}}T$
所以月球的角速度ω=$\frac{2π}{T}$,
“嫦娥二号”的角速度ω′=$\frac{2π}{T′}$
由于“嫦娥二号”绕月与月绕地的转动方向同向,所以有π=(ω′-ω)•△t
即$π=(\frac{2π}{\sqrt{\frac{k}{{n}^{3}}}T}-\frac{2π}{T})△t$
所以△t$\frac{T}{2(\sqrt{\frac{{n}^{3}}{k}}-1)}$,故B正确,ACD错误.
本题选错误的,故选:ACD.
点评 本题首先要注意向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用,其次要注意“嫦娥二号”绕月与月绕地的转动方向同向,所以从“嫦娥二号”距地球最远到距离地球最近转过的角度为π,有π=(ω′-ω)•△t.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案 假设月球半径为R,月球表面的重力加速度为g0,如图所示,飞船首先沿距月球表面高度为3R的圆轨道I运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(轨道半径可近似当做R)绕月球做圆周运动.下列判断正确的是( )
假设月球半径为R,月球表面的重力加速度为g0,如图所示,飞船首先沿距月球表面高度为3R的圆轨道I运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(轨道半径可近似当做R)绕月球做圆周运动.下列判断正确的是( )| A. | 飞船在轨道 I上的运行速率为$\sqrt{{g}_{0}R}$ | |
| B. | 飞船在轨道Ⅲ绕月球运动一周所需的时间为2π$\sqrt{\frac{R}{{g}_{0}}}$ | |
| C. | 飞船在Ⅱ轨道A点速率大于在Ⅰ轨道A点速率 | |
| D. | 飞船在Ⅱ轨道B点加速度大于Ⅲ轨道B点加速度 |
 如图所示,船在A处开出后沿直线AB到达对岸,若AB与河岸成37°角,水流速度为4m/s,则船相对静水最小速度为( )
如图所示,船在A处开出后沿直线AB到达对岸,若AB与河岸成37°角,水流速度为4m/s,则船相对静水最小速度为( )| A. | 2m/s | B. | 2.4m/s | C. | 3m/s | D. | 3.5m/s |

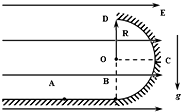 如图,ABCD为表示竖立放在场强为E=104V/m的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环,轨道的水平部分与圆环相切,A为水平轨道的一点,而且AB=R=0.2m把一质量m=0.1kg、带电q=10-4C的小球,放在水平轨道的A点上面由静止开始被释放后,在轨道的内侧运动.(g取10m/s2)求:
如图,ABCD为表示竖立放在场强为E=104V/m的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环,轨道的水平部分与圆环相切,A为水平轨道的一点,而且AB=R=0.2m把一质量m=0.1kg、带电q=10-4C的小球,放在水平轨道的A点上面由静止开始被释放后,在轨道的内侧运动.(g取10m/s2)求: 如图,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g.
如图,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g. 倾角为θ的斜面上只有AB段粗糙,动摩擦因数为μ=2tanθ,其余部分光滑.AB段长为2L,有N个相同的小木块(单独考虑每个小木块时,视为质点)沿斜面靠在一起,但不粘接,总长为L,每一个小木块的质量均为m,将它们由静止释放,释放时下端距A为2L,B到斜面底端足够长.求:
倾角为θ的斜面上只有AB段粗糙,动摩擦因数为μ=2tanθ,其余部分光滑.AB段长为2L,有N个相同的小木块(单独考虑每个小木块时,视为质点)沿斜面靠在一起,但不粘接,总长为L,每一个小木块的质量均为m,将它们由静止释放,释放时下端距A为2L,B到斜面底端足够长.求: