题目内容
15. 如图所示,一半径为R的绝缘圆形轨道竖直放置,圆形轨道的最低点与一水平轨道相连,轨道都是光滑的,轨道所在的空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m的带正电的小球,为使小球刚好能在竖直面内完成圆周运动,求释放点A距圆轨道最低点B的距离s.已知小球受的电场力等于小球重力的$\frac{3}{4}$.
如图所示,一半径为R的绝缘圆形轨道竖直放置,圆形轨道的最低点与一水平轨道相连,轨道都是光滑的,轨道所在的空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m的带正电的小球,为使小球刚好能在竖直面内完成圆周运动,求释放点A距圆轨道最低点B的距离s.已知小球受的电场力等于小球重力的$\frac{3}{4}$.
分析 小球刚好在圆轨道内完成圆周运动,在最高点,重力提供向心力,由牛顿第二定律与动能定理可以求出S大小.
解答 解:小球在最高点,如图所示,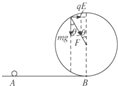
已知:qE=$\frac{3}{4}$mg,则重力与电场力的合力:F=$\sqrt{(mg)^{2}+(\frac{3}{4}mg)^{2}}$=$\frac{5}{4}$mg,
小球刚好在圆轨道内做圆周运动,在最高点,弹力为零,重力与电场力的合力提供向心力,
由牛顿第二定律得:F=m$\frac{{v}^{2}}{R}$,解得:v=$\sqrt{\frac{5}{4}gR}$,
小球从水平轨道到达最高点过程中,
由动能定理得:qEs-mgR(1+cosθ)-qERsinθ=$\frac{1}{2}$mv2-0,
已知:qE=$\frac{3}{4}$mg,sinθ=$\frac{qE}{F}$=$\frac{\frac{3}{4}mg}{\frac{5}{4}mg}$=$\frac{3}{5}$,cosθ=$\frac{4}{5}$,
解得:s=$\frac{23R}{6}$;
答:释放点A距圆轨道最低点B的距离为$\frac{23R}{6}$.
点评 本题难度不大,确定物体运动过程,应用动能定理与牛顿第二定律即可正确解题;解题时要注意“小球刚好在圆轨道内完成圆周运动”的隐含信息.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
5.一个电荷只在电场力作用下从电场中的A点移到B点时,电场力做了5×10-6J的功,那么( )
| A. | 电荷的电势能增加了5×10-6J | |
| B. | 电荷的电势能减少了5×10-6J | |
| C. | 电荷在B处时将具有5×10-6J的电势能 | |
| D. | 电荷在B处将具有5×10-6J的动能 |
3. 摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶.如图所示,若特技演员质量m=50kg,导演在某房顶离地H=12m处架设了轮轴(轮与轴有相同的角速度),轮和轴的直径之比为3:2(人和车均视为质点,且轮轴直径远小于H),若轨道车从图中A前进到B,在B处时,速度v=10m/s,绳BO与水平方向的夹角为53°,则由于绕在轮上细钢丝的拉动,使演员由地面从静止开始向上运动.在车从A运动到B的过程中(g取10m/s2)( )
摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶.如图所示,若特技演员质量m=50kg,导演在某房顶离地H=12m处架设了轮轴(轮与轴有相同的角速度),轮和轴的直径之比为3:2(人和车均视为质点,且轮轴直径远小于H),若轨道车从图中A前进到B,在B处时,速度v=10m/s,绳BO与水平方向的夹角为53°,则由于绕在轮上细钢丝的拉动,使演员由地面从静止开始向上运动.在车从A运动到B的过程中(g取10m/s2)( )
 摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶.如图所示,若特技演员质量m=50kg,导演在某房顶离地H=12m处架设了轮轴(轮与轴有相同的角速度),轮和轴的直径之比为3:2(人和车均视为质点,且轮轴直径远小于H),若轨道车从图中A前进到B,在B处时,速度v=10m/s,绳BO与水平方向的夹角为53°,则由于绕在轮上细钢丝的拉动,使演员由地面从静止开始向上运动.在车从A运动到B的过程中(g取10m/s2)( )
摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶.如图所示,若特技演员质量m=50kg,导演在某房顶离地H=12m处架设了轮轴(轮与轴有相同的角速度),轮和轴的直径之比为3:2(人和车均视为质点,且轮轴直径远小于H),若轨道车从图中A前进到B,在B处时,速度v=10m/s,绳BO与水平方向的夹角为53°,则由于绕在轮上细钢丝的拉动,使演员由地面从静止开始向上运动.在车从A运动到B的过程中(g取10m/s2)( )| A. | 演员上升的高度为3m | |
| B. | 演员最大速度为6m/s | |
| C. | 以地面为重力势能的零点,演员最大机械能为2400J | |
| D. | 钢丝在这一过程中对演员做功为4275J |
7. 如图所示,质量为M的四分之一圆柱体放在粗糙水平地面上,质量为m的正方体放在圆柱体和光滑墙壁之间,且不计圆柱体与正方体之间的摩擦,正方体与圆柱体的接触点的切线与右侧墙壁成θ角,圆柱体处于静止状态.则( )
如图所示,质量为M的四分之一圆柱体放在粗糙水平地面上,质量为m的正方体放在圆柱体和光滑墙壁之间,且不计圆柱体与正方体之间的摩擦,正方体与圆柱体的接触点的切线与右侧墙壁成θ角,圆柱体处于静止状态.则( )
 如图所示,质量为M的四分之一圆柱体放在粗糙水平地面上,质量为m的正方体放在圆柱体和光滑墙壁之间,且不计圆柱体与正方体之间的摩擦,正方体与圆柱体的接触点的切线与右侧墙壁成θ角,圆柱体处于静止状态.则( )
如图所示,质量为M的四分之一圆柱体放在粗糙水平地面上,质量为m的正方体放在圆柱体和光滑墙壁之间,且不计圆柱体与正方体之间的摩擦,正方体与圆柱体的接触点的切线与右侧墙壁成θ角,圆柱体处于静止状态.则( )| A. | 地面对圆柱体的支持力为Mg | B. | 地面对圆柱体的摩擦力为mgtanθ | ||
| C. | 墙壁对正方体的弹力为$\frac{mg}{tanθ}$ | D. | 正方体对圆柱体的压力为$\frac{mg}{cosθ}$ |
4. 如图为一空间探测器的示意图,P1、P2、P3、P4是四个喷气发动机,每台发动机开动时都能提供推力,但不会使探测器转动,开始时探测器以恒定速度v0向正X方向运动.则( )
如图为一空间探测器的示意图,P1、P2、P3、P4是四个喷气发动机,每台发动机开动时都能提供推力,但不会使探测器转动,开始时探测器以恒定速度v0向正X方向运动.则( )
 如图为一空间探测器的示意图,P1、P2、P3、P4是四个喷气发动机,每台发动机开动时都能提供推力,但不会使探测器转动,开始时探测器以恒定速度v0向正X方向运动.则( )
如图为一空间探测器的示意图,P1、P2、P3、P4是四个喷气发动机,每台发动机开动时都能提供推力,但不会使探测器转动,开始时探测器以恒定速度v0向正X方向运动.则( )| A. | 单独分别开动P1、P2、P3、P4喷气发动机,探测器均作直线运动 | |
| B. | 单独分别开动P1、P3喷气发动机,探测器均作直线运动 | |
| C. | 单独分别开动P2、P4喷气发动机,探测器均作曲线运动 | |
| D. | 同时开动P1、P2喷气发动机,探测器作曲线运动 |

 如图,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g.
如图,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g.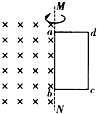 如图所示的空间存在一匀强磁场,其方向为垂直于纸面向里,磁场的右边界为MN,在MN右侧有一矩形金属线圈abcd,ab边与MN重合.现使线圈以ab边为轴按图示方向匀速转动,将a、b两端连到示波器的输入端,若电势a高b低时uab为正,则从下列图中示波器观察到的uab随时间变化的规律是 ( )
如图所示的空间存在一匀强磁场,其方向为垂直于纸面向里,磁场的右边界为MN,在MN右侧有一矩形金属线圈abcd,ab边与MN重合.现使线圈以ab边为轴按图示方向匀速转动,将a、b两端连到示波器的输入端,若电势a高b低时uab为正,则从下列图中示波器观察到的uab随时间变化的规律是 ( )



 用如图所示的多用电表测量电阻,要用到选择开关K和两个部件S、T.请根据下列五个步骤完成电阻测量:
用如图所示的多用电表测量电阻,要用到选择开关K和两个部件S、T.请根据下列五个步骤完成电阻测量: