题目内容
17．
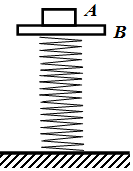一理想弹簧下端固定在水平地面上，上端与质量为2kg的物体B栓接，再把另一质量为lkg的物体A放在B上，静止在图示位置．现对A施加一竖直向上的力F，欲使在施加力的瞬间，A、B即开始分离，则F的最小值为（g=10m/s2）（ ）| A． | l0N | |
| B． | 15N | |
| C． | 20N | |
| D． | 满足要求的F的最小值与弹簧的劲度系数有关 |
分析 A、B刚开始分离时，两者间的弹力为零，分别以整体和A为研究对象，根据牛顿第二定律列式，可求得F的最小值．
解答 解：当A、B刚开始分离时F最小．根据牛顿第二定律，对AB整体有：
F=（mA+mB）a
对A有：F-mAg=mAa
联立解得，F的最小值为：F=$\frac{{m}_{A}（{m}_{A}+{m}_{B}）g}{{m}_{B}}$=$\frac{1×（1+2）×10}{2}$N=15N，可知F与与弹簧的劲度系数无关．故B正确，ACD错误．
故选：B
点评 本题是连接体问题，关键要抓住两个物体的加速度相同，刚分离时两者之间的弹力为零．要灵活选择研究对象，采用整体法和隔离法结合研究比较简洁．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
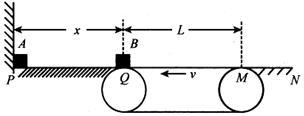
7．
如图，一轻弹簧一端固定在墙角上，另一端自由，整个弹簧放在水平粗糙地面上，现用一木块向右将弹簧压缩一段距离后释放，则从刚释放一直到木块刚脱离弹簧的过程中，有关木块的运动下列说法正确的是（ ）
如图，一轻弹簧一端固定在墙角上，另一端自由，整个弹簧放在水平粗糙地面上，现用一木块向右将弹簧压缩一段距离后释放，则从刚释放一直到木块刚脱离弹簧的过程中，有关木块的运动下列说法正确的是（ ）| A． | 加速度先变小后变大 | B． | 加速度一直变小 | ||
| C． | 速度先变大后变小 | D． | 速度一直变大 |
8．做匀速圆周运动的物体所需向心力的方向（ ）
| A． | 一定与物体的速度方向相同 | |
| B． | 一定与物体的速度方向相反 | |
| C． | 一定与物体的速度方向垂直 | |
| D． | 与物体的速度方向有时相同、有时相反 |
12．人造卫星a的圆形轨道离地面高度为h，地球同步卫星b离地面高度为H，h＜H，两卫星共面且旋转方向相同．某时刻卫星a恰好出现在赤道上某建筑物c的正上方，设地球赤道半径为R，地面重力加速度为g，则（ ）
| A． | a、b线速度大小之比为$\sqrt{\frac{R+h}{R+H}}$ | |
| B． | a、c角速度之比为$\sqrt{\frac{{R}^{3}}{（R+h）^{3}}}$ | |
| C． | b、c向心加速度大小之比$\frac{R+H}{R}$ | |
| D． | a下一次通过c正上方所需时间等于t=2π$\sqrt{\frac{（R+h）^{3}}{g{R}^{2}}}$ |
如图所示质量为2kg的小球以10m/s竖直向上运动，当小球落回到出发位置时速度大小变为5m/s，试求：