题目内容
13. 如图所示质量为2kg的小球以10m/s竖直向上运动,当小球落回到出发位置时速度大小变为5m/s,试求:
如图所示质量为2kg的小球以10m/s竖直向上运动,当小球落回到出发位置时速度大小变为5m/s,试求:(1)空气阻力
(2)上升的最大高度
(3)整个运动时间.
分析 (1)分别对小球的全过程和上升过程运用动能定理,求出小球在运动过程中所受空气的平均阻力的大小.
(2)对上升的过程(或下降的过程)应用动能定理即可求出上升的最大高度;
(3)由动量定理分别求出上升的时间和下落的时间,再求和即可.
解答 解:(1)设小球受到的阻力为F,上升的最大高度为h,由动能定理,对全过程有:-F•2h=$\frac{1}{2}$m(0.5v0)2-$\frac{1}{2}$mv02 ①
对上升过程有:-mgh-Fh=0-$\frac{1}{2}$mv02. ②
由以上两式可解得:F=0.6mg=0.6×2×10=12N.
(2)将F=12N代入②,可得:h=3.125m
(3)取向下是方向为正方向,设上升的时间为t1,下落的时间为t2,由动量定理得,上升的过程:(mg+F)t1=0-mv0
代入数据得:${t}_{1}=\frac{5}{8}$s
下落的过程:$(mg-F){t}_{2}=\frac{1}{2}m{v}_{0}-0$
代入数据得:${t}_{2}=\frac{5}{4}$s
总时间:$t={t}_{1}+{t}_{2}=\frac{5}{8}+\frac{5}{4}=\frac{15}{8}$s=1.875s
答:(1)空气阻力大小是12N;
(2)上升的最大高度是3.125m;
(3)整个运动时间是1.875s.
点评 运用动能定理解题关键确定好研究的过程,分析过程中有哪些力做功,然后根据动能定理列式求解,难度不大.
其中第三问也可以由牛顿第二定律分别求出上升的加速度与下降的加速度,然后由运动学的公式求出时间,再求和即可.

练习册系列答案
相关题目
17.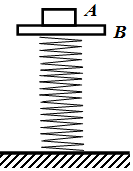 一理想弹簧下端固定在水平地面上,上端与质量为2kg的物体B栓接,再把另一质量为lkg的物体A放在B上,静止在图示位置.现对A施加一竖直向上的力F,欲使在施加力的瞬间,A、B即开始分离,则F的最小值为(g=10m/s2)( )
一理想弹簧下端固定在水平地面上,上端与质量为2kg的物体B栓接,再把另一质量为lkg的物体A放在B上,静止在图示位置.现对A施加一竖直向上的力F,欲使在施加力的瞬间,A、B即开始分离,则F的最小值为(g=10m/s2)( )
 一理想弹簧下端固定在水平地面上,上端与质量为2kg的物体B栓接,再把另一质量为lkg的物体A放在B上,静止在图示位置.现对A施加一竖直向上的力F,欲使在施加力的瞬间,A、B即开始分离,则F的最小值为(g=10m/s2)( )
一理想弹簧下端固定在水平地面上,上端与质量为2kg的物体B栓接,再把另一质量为lkg的物体A放在B上,静止在图示位置.现对A施加一竖直向上的力F,欲使在施加力的瞬间,A、B即开始分离,则F的最小值为(g=10m/s2)( )| A. | l0N | |
| B. | 15N | |
| C. | 20N | |
| D. | 满足要求的F的最小值与弹簧的劲度系数有关 |
18.下列说法正确的是( )
| A. | 放射性元素与别的元素形成化合物时就不具有放射性 | |
| B. | 一个氢原子从 n=3 的能级跃迁的 n=2 的能级,该氢原子放出光子,电子动能增加,总能量增加 | |
| C. | 原子从 a 能级状态跃迁到 b 能级状态时发射波长为λ1 的光子,原子从 b 能级状态跃迁到 c 能级状态时发射波长为λ2 的光子,已知λ1>λ2,那么原子从 a 能级状态跃迁到 c 能级状态时发射波长为 $\frac{{λ}_{1}{λ}_{2}}{{λ}_{1}-{λ}_{2}}$ 的光子 | |
| D. | 放射性的原子核发生衰变后产生的新核从高能级向低能级跃迁时,辐射出 γ 射线 |
18. 如图所示,在空间存在竖直向上的匀强电场,质量为m、电荷量为q的物块,从A点由静止开始向下做加速度为$\frac{g}{3}$匀加速直线运动,下落高度H到达B点后与一轻弹簧接触,又下落h后到达最低点C,整个过程中不计空气阻力,且弹簧始终在弹性限度内,g为重力加速度,在物块由A点运动到C的过程中( )
如图所示,在空间存在竖直向上的匀强电场,质量为m、电荷量为q的物块,从A点由静止开始向下做加速度为$\frac{g}{3}$匀加速直线运动,下落高度H到达B点后与一轻弹簧接触,又下落h后到达最低点C,整个过程中不计空气阻力,且弹簧始终在弹性限度内,g为重力加速度,在物块由A点运动到C的过程中( )
 如图所示,在空间存在竖直向上的匀强电场,质量为m、电荷量为q的物块,从A点由静止开始向下做加速度为$\frac{g}{3}$匀加速直线运动,下落高度H到达B点后与一轻弹簧接触,又下落h后到达最低点C,整个过程中不计空气阻力,且弹簧始终在弹性限度内,g为重力加速度,在物块由A点运动到C的过程中( )
如图所示,在空间存在竖直向上的匀强电场,质量为m、电荷量为q的物块,从A点由静止开始向下做加速度为$\frac{g}{3}$匀加速直线运动,下落高度H到达B点后与一轻弹簧接触,又下落h后到达最低点C,整个过程中不计空气阻力,且弹簧始终在弹性限度内,g为重力加速度,在物块由A点运动到C的过程中( )| A. | 物块所受的电场力大小为$\frac{2mg}{3}$ | B. | 物块动能的最大值为$\frac{mgH}{3}$ | ||
| C. | 物块电势能的减少量为$\frac{mg(H+h)}{2}$ | D. | 弹簧弹性势能的增加量为$\frac{mg(H+h)}{3}$ |
5.轻弹簧竖立在地面上,其周围存在竖直方向的匀强电场,忽略空气阻力.让一带电物块自弹簧上方某位置由静止释放,在A处接触弹簧,自A运动到B的过程中,重力做功8J,电场力做功5J,物块克服弹簧弹力做功6J.则从A到B的过程中,对物块、弹簧、地球组成的系统( )
| A. | 重力势能减少8J | B. | 电势能增加5J | C. | 动能增加7J | D. | 机械能增加5J |
3.以下关于光学知识的叙述中,正确的是( )


| A. | 甲图是著名的泊松亮斑图案,这是光波的衍射现象 | |
| B. | 乙图中的彩虹是不同色光在水滴中折射率不同造成的 | |
| C. | 丙图的照相机镜头上涂有一层增透膜,增透膜利用了光的偏振原理 | |
| D. | 丁图是医学上的内窥镜,其核心部件光导纤维能传输光像信号,是利用光的全反射 |
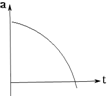
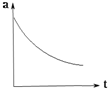
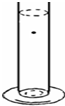 球体在液体中下落时,液体对球的粘滞阻力与球的半径、速度及液体的种类有关,有F=6πηrv,其中物理量η为液体的粘滞系数,它还与液体的种类及温度有关,如图所示,现将一颗小钢珠由静止释放到盛有蓖麻油的足够深量筒中,下列描绘小钢珠在下沉过程中加速度大小与时间关系的图象可能正确的是( )
球体在液体中下落时,液体对球的粘滞阻力与球的半径、速度及液体的种类有关,有F=6πηrv,其中物理量η为液体的粘滞系数,它还与液体的种类及温度有关,如图所示,现将一颗小钢珠由静止释放到盛有蓖麻油的足够深量筒中,下列描绘小钢珠在下沉过程中加速度大小与时间关系的图象可能正确的是( )