题目内容
9.如图,长度x=5m的粗糙水平面PQ的左端固定一竖直挡板,右端Q处与水平传送带平滑连接,传送带以一定速率v逆时针转动,其上表面QM间距离为L=4m,MN无限长,M端与传送带平滑连接.物块A和B可视为质点,A的质量m=1.5kg,B的质量M=5.5kg.开始A静止在P处,B静止在Q处,现给A一个向右的初速度vo=8m/s,A运动一段时间后与B发生弹性碰撞,设A、B与传送带和水平面PQ、MN间的动摩擦因数均为μ=0.15,A与挡板的碰撞也无机械能损失.取重力加速度g=10m/s2,求: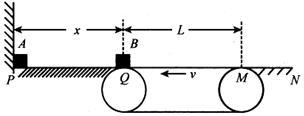
(1)A、B碰撞后瞬间的速度大小;
(2)若传送带的速率为v=4m/s,试判断A、B能否再相遇,如果能相遇,求出相遇的位置;若不能相遇,求它们最终相距多远.
分析 (1)根据动能定理求出A与B碰撞前瞬间的速度,再根据动量守恒定律和能量守恒定律求出A、B碰撞后瞬间的速度大小;
(2)根据动能定理求出A碰撞后运动的路程,以及碰撞后向右运动的距离,判断出不能滑上MN,之后向左运动,再次到达Q处,根据位移关系分析AB能否再次相遇.
解答 解:(1)设A与B碰撞前的速度为vA,由P到Q的过程,由动能定理得:
-μmgx=$\frac{1}{2}$mvA2-$\frac{1}{2}$mv02.①
A与B碰撞前后动量守恒,取向右为正方向,则 mvA=mvA′+MvB′②
由能量守恒定律得 $\frac{1}{2}$mvA2=$\frac{1}{2}$mvA′2+$\frac{1}{2}$MvB′2. ③
联立①②③得 vA′=-4m/s,vB′=3m/s.
(2)设A碰撞后运动的路程为sA,由动能定理得:
-μmgsA=0-$\frac{1}{2}$mvA′2.④
解得 sA=$\frac{16}{3}$m
所以A与挡板碰撞后再运动的距离 sA′=sA-x=$\frac{16}{3}$-5=$\frac{1}{3}$m ⑤
设B碰撞后向右运动的距离为sB,由动能定理得:
-μMgsB=0-$\frac{1}{2}$MvB′2.⑥
解得 sB=3m<L ⑦
故物块B碰后不能滑上MN,当速度减为0后,B将在传送带的作用下反向加速运动,B再次到达Q处时的速度大小为3m/s.
在水平PQ上,B再运动 sB′=sB=3m停止,因为 sA′+sB′<x=5m,所以AB不能再次相遇,最终AB间的距离 sAB=x-(sA′+sB′)=5-($\frac{1}{3}$+3)=$\frac{5}{3}$m
答:
(1)A、B碰撞后瞬间的速度大小分别是4m/s和3m/s.
(2)AB不能再次相遇,最终AB间的距离是$\frac{5}{3}$m.
点评 解决本题的关键是要理清A、B在整个过程中的运动情况,抓住碰撞的规律:动量守恒定律及能量守恒定律,知道涉及空间距离时,运用动能定理求解比较简便.

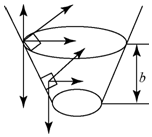 有一种杂技表演叫“飞车走璧”.由杂技赏驾驶摩托车沿置台形表演台的侧量高速行驶,做匀速圆周运动.如图所示,图中虚线表示摩托车的行驶轨道,轨迹离地面的高度为h,下列说法中正确的是( )
有一种杂技表演叫“飞车走璧”.由杂技赏驾驶摩托车沿置台形表演台的侧量高速行驶,做匀速圆周运动.如图所示,图中虚线表示摩托车的行驶轨道,轨迹离地面的高度为h,下列说法中正确的是( )| A. | h越高,摩托车对侧璧的压力将越大 | |
| B. | h越高,摩托车做圆周运动的向心力将越大 | |
| C. | h越高,摩托车做运动的线速度将越大 | |
| D. | h越高,摩托车做圆周运动的周期将越大 |
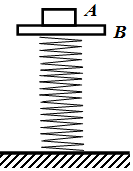 一理想弹簧下端固定在水平地面上,上端与质量为2kg的物体B栓接,再把另一质量为lkg的物体A放在B上,静止在图示位置.现对A施加一竖直向上的力F,欲使在施加力的瞬间,A、B即开始分离,则F的最小值为(g=10m/s2)( )
一理想弹簧下端固定在水平地面上,上端与质量为2kg的物体B栓接,再把另一质量为lkg的物体A放在B上,静止在图示位置.现对A施加一竖直向上的力F,欲使在施加力的瞬间,A、B即开始分离,则F的最小值为(g=10m/s2)( )| A. | l0N | |
| B. | 15N | |
| C. | 20N | |
| D. | 满足要求的F的最小值与弹簧的劲度系数有关 |
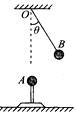 有三个完全相同的金属小球A、B、C,其中小球C不带电,小球A和B带有等量的同种电荷,如图所示,A球固定在竖直支架上,B球用不可伸长的绝缘细线悬于A球正上方的P点处,静止时细线与OA的夹角为θ.小球C可用绝缘手柄移动,重力加速度为g,现在进行下列操作,其中描述与事实相符的是( )
有三个完全相同的金属小球A、B、C,其中小球C不带电,小球A和B带有等量的同种电荷,如图所示,A球固定在竖直支架上,B球用不可伸长的绝缘细线悬于A球正上方的P点处,静止时细线与OA的夹角为θ.小球C可用绝缘手柄移动,重力加速度为g,现在进行下列操作,其中描述与事实相符的是( )| A. | 仅将球C与球A接触离开后,B球再次静止时细线中的张力比原来要小 | |
| B. | 仅将球C与球A接触离开后,B球再次静止时细线与OA的夹角为θ1,仅将球C与球A接触离开后,B球再次静止时细线与OA的夹角为θ2,则θ1=θ2 | |
| C. | 剪断细线OB瞬间,球B的加速度等于g | |
| D. | 剪断细线OB后,球B将沿OB方向做匀变速直线运动直至着地 |
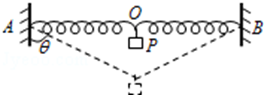 如图所示,长为2L的轻弹簧AB两端等高的固定在竖直墙面上,弹簧刚好处于原长,现在其中点O处轻轻地挂上一个质量为m的物体P后,物体向下运动,当它运动到最低点时,弹簧与竖直方向的夹角为θ,重力加速度为g,下列说法正确的是( )
如图所示,长为2L的轻弹簧AB两端等高的固定在竖直墙面上,弹簧刚好处于原长,现在其中点O处轻轻地挂上一个质量为m的物体P后,物体向下运动,当它运动到最低点时,弹簧与竖直方向的夹角为θ,重力加速度为g,下列说法正确的是( )| A. | 向下运动的过程中,物体的加速度先增大后减小 | |
| B. | 向下运动的过程中,物体的机械能先增大后减小 | |
| C. | 物体在最低点时,弹簧的弹性势能为$\frac{mgL}{tanθ}$ | |
| D. | 物体在最低点时,弹簧中的弹力为$\frac{mg}{2cosθ}$ |

| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
| A. | 放射性元素与别的元素形成化合物时就不具有放射性 | |
| B. | 一个氢原子从 n=3 的能级跃迁的 n=2 的能级,该氢原子放出光子,电子动能增加,总能量增加 | |
| C. | 原子从 a 能级状态跃迁到 b 能级状态时发射波长为λ1 的光子,原子从 b 能级状态跃迁到 c 能级状态时发射波长为λ2 的光子,已知λ1>λ2,那么原子从 a 能级状态跃迁到 c 能级状态时发射波长为 $\frac{{λ}_{1}{λ}_{2}}{{λ}_{1}-{λ}_{2}}$ 的光子 | |
| D. | 放射性的原子核发生衰变后产生的新核从高能级向低能级跃迁时,辐射出 γ 射线 |
| A. | 重力势能减少8J | B. | 电势能增加5J | C. | 动能增加7J | D. | 机械能增加5J |
 风洞可产生方向、大小都可以调节控制的各种风力.如图所示为风洞里模拟实验的示意图.一质量为m=1kg的实验对象(可视为质点)套在一根固定的直杆上,直杆与水平面夹角为θ=30°.风洞产生竖直向上的、大小F=20N的风力作用在实验对象上,实验对象从M点由静止开始沿直杆向上运动.已知实验对象与杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$.取g=10m/s2.求:
风洞可产生方向、大小都可以调节控制的各种风力.如图所示为风洞里模拟实验的示意图.一质量为m=1kg的实验对象(可视为质点)套在一根固定的直杆上,直杆与水平面夹角为θ=30°.风洞产生竖直向上的、大小F=20N的风力作用在实验对象上,实验对象从M点由静止开始沿直杆向上运动.已知实验对象与杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$.取g=10m/s2.求: