题目内容
10.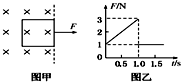 一正方形金属线框位于有界匀强磁场区域内,线框平面与磁场垂直,线框的右边紧贴着磁场边界,如图甲所示.t=0时刻对线框施加一水平向右的外力,让线框从静止开始做匀加速直线运动穿过磁场,外力F随时间t变化的图象如图乙所示.已知线框质量m=1kg、电阻R=1Ω,以下说法错误的是( )
一正方形金属线框位于有界匀强磁场区域内,线框平面与磁场垂直,线框的右边紧贴着磁场边界,如图甲所示.t=0时刻对线框施加一水平向右的外力,让线框从静止开始做匀加速直线运动穿过磁场,外力F随时间t变化的图象如图乙所示.已知线框质量m=1kg、电阻R=1Ω,以下说法错误的是( )| A. | 线框做匀加速直线运动的加速度为1m/s2 | |
| B. | 匀强磁场的磁感应强度为2$\sqrt{2}$T | |
| C. | 线框穿过磁场的过程中,通过线框的电荷量为$\frac{\sqrt{2}}{2}$C | |
| D. | 线框边长为1m |
分析 当t=0时线框的速度为零,没有感应电流,线框不受安培力,根据牛顿第二定律求出加速度a.
由运动学公式求出线框刚出磁场时的速度,得到安培力表达式,由牛顿第二定律即可求出B;
根据法拉第电磁感应定律、欧姆定律结合求解电量.由运动学规律求线框的边长.
解答 解:A、t=0时刻,线框的速度为零,线框中没有感应电流,不受安培力,则其加速度为:a=$\frac{F}{m}$=$\frac{1}{1}$=1m/s2,故A正确;
BD、线框的边长为:L=$\frac{1}{2}$at2=$\frac{1}{2}$×1×12=0.5m.线框刚出磁场时的速度为 v=at=1×1m/s=1m/s,此时线框所受的安培力为FA=BIL,I=$\frac{BLv}{R}$,则得 FA=$\frac{{B}^{2}{L}^{2}v}{R}$,根据牛顿第二定律得 F-FA=ma,代入得 F-$\frac{{B}^{2}{L}^{2}v}{R}$=ma,代入数据 F=3N,m=1kg,R=1Ω,L=0.5m,v=1m/s,a=1m/s2解得:B=2$\sqrt{2}$T,故B正确,D错误;
C、通过线框的电荷量:q=$\overline{I}$t=$\frac{\overline{E}}{R}$t=$\frac{BL\overline{v}t}{R}$=$\frac{B{L}^{2}}{R}$=$\frac{2\sqrt{2}×0.{5}^{2}}{1}$=$\frac{\sqrt{2}}{2}$C,故C正确.
本题选错误的,故选:D
点评 本题的突破口是根据牛顿第二定律求出加速度,根据运动学公式求出线框的边长和速度,问题就变得简单清晰了,再根据法拉第电磁感应定律、欧姆定律、安培力公式等等电磁感应常用的规律解题.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案 如图所示,固定在竖直平面内的$\frac{1}{4}$光滑圆管轨道ABCD,其A点与圆心等高,D点为最高点,今使质量为m的小球自A点正上方h高处由静止释放,且从A处进入圆管轨道并经过D点刚好落回A点,则下列说法中正确的是( )
如图所示,固定在竖直平面内的$\frac{1}{4}$光滑圆管轨道ABCD,其A点与圆心等高,D点为最高点,今使质量为m的小球自A点正上方h高处由静止释放,且从A处进入圆管轨道并经过D点刚好落回A点,则下列说法中正确的是( )| A. | 只要h>R小球就会落回到A点 | |
| B. | 当h≥$\frac{5R}{4}$时小球一定过最高点D并落回到A点 | |
| C. | 当小球刚好落回到A点时小球在D点所受的弹力大小为$\frac{mg}{2}$,方向向上 | |
| D. | 若将圆管改成光滑圆轨道,只要调整h的大小,小球从D点出来后也能落到A点 |
(1)实验的部分步骤如下:
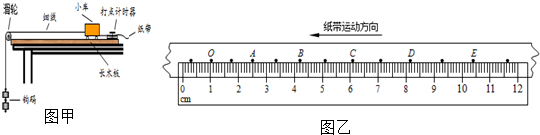
①实验前先将长木板右端适当垫高,使小车刚好能沿木板匀速下滑;
②在小车中放入砝码,让纸带穿过打点计时器,连在小车后端,用细线连接小车和钩码;
③将小车停在靠近打点计时器处,先接通电源,后释放小车,小车拖动纸带运动,打点计时器在纸带上打下一系列点,关闭电源;
④改变钩码或小车中砝码的数量,更换纸带,重复③的操作.
(2)如图乙所示是某次实验得到的一条纸带,在纸带上选择起始点O及多个计数点A、B、C、D、E、…,可获得各计数点刻度值x,求出对应时刻小车的瞬时速度v,则D点对应的刻度值为xD=8.15cm,D点对应的速度大小为vD=0.54m/s.
(3)下表是某同学在改变钩码或小车中砝码的数量时得到的数据.其中M是小车质量M1与小车中砝码质量m之和,|v22-v12|是纸带上某两点速度的平方差,可以据此计算出动能变化量△Ek;F是钩码所受重力的大小,W是以上两点间F所做的功.
| 次数 | M/kg | |v22-v12|/(m2/s-2) | △Ek/J | F/N | W/J |
| 1 | 0.500 | 0.76 | 0.190 | 0.490 | 0.210 |
| 2 | 0.500 | 1.65 | 0.413 | 0.980 | 0.430 |
| 3 | 0.500 | 2.40 | 0.600 | 1.470 | 0.630 |
| 4 | 1.000 | 2.40 | 1.200 | 2.450 | 1.240 |
| 5 | 1.000 | 2.84 | 1.420 | 2.940 | 1.470 |
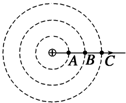 如图所示,三个同心圆是一个点电荷周围的三个等势面,已知这三个圆半径之差相等.A、B、C分别是这三个等势面上的点,且在同一条电场线上.A、C两点的电势依次为φA=20V和φC=10V,则B点的电势( )
如图所示,三个同心圆是一个点电荷周围的三个等势面,已知这三个圆半径之差相等.A、B、C分别是这三个等势面上的点,且在同一条电场线上.A、C两点的电势依次为φA=20V和φC=10V,则B点的电势( )| A. | 可能等于15V | B. | 可能大于15V | C. | 一定小于15V | D. | 无法判断 |
| A. | 在光的折射中,入射角与折射角成正比 | |
| B. | 变化的磁场产生电场 | |
| C. | 光纤通信利用了全反射的原理 | |
| D. | 光的衍射说明光是横波 | |
| E. | 双缝干涉实验中,若只是两缝间的距离增大,同种色光干涉条纹的相邻条纹间距减小 |
| A. | 庐山发生了变化 | B. | 诗人心情发生了变化 | ||
| C. | 把庐山看成了质点 | D. | 没有把庐山看成质点 |
 将长度为2m的导线弯折成等长的两段AB和BC,∠ABC=120°,如图所示,现将它放置在磁感应强度B=1T的匀强磁场中,并使之以v=10m/s的速率在纸面内平动,那么A、C两端可能出现的电势差的大小|UAC|的最大值为10$\sqrt{3}$V,最小值为0V.
将长度为2m的导线弯折成等长的两段AB和BC,∠ABC=120°,如图所示,现将它放置在磁感应强度B=1T的匀强磁场中,并使之以v=10m/s的速率在纸面内平动,那么A、C两端可能出现的电势差的大小|UAC|的最大值为10$\sqrt{3}$V,最小值为0V.