题目内容
【题目】如图所示,质量为m=2kg的物块放在一固定斜面上,斜面长L=11m,当斜面倾角为37°时物块恰能沿斜面匀速下滑.现对物体施加一大小为F=100N的水平向右恒力,可使物体从斜面底端由静止开始向上滑行,求(已知sin37°=0.6,cos37°=0.8,g=10m/s2)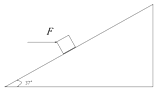
(1)物块在F力作用下从斜面底端运动到顶端所需的时间;
(2)若要在F力作用下保证物块可以从斜面底端运动到顶端,则该力作用的最短时间是多少?
【答案】
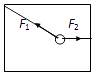
(1)解:物体匀速下滑时,受力如下图所示:
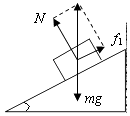
根据平衡条件得:
mgsin37°=f1
N=mgcos37°
又 f1=μN
所以μ=tan37°=0.75;
物体沿斜面上升,受力如图所示:
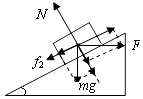
则有Fcos37°﹣μ(Fsin37°+mgcos37°)﹣mgsin37°=ma
解得:a=5.5m/s2;
由位移公式L= ![]() at2可得:t=
at2可得:t= ![]() =
= ![]() =2s
=2s
答:物块在F力作用下从斜面底端运动到顶端所需的时间2s
(2)解:当物体到达顶端速度恰好为零时,F的作用时间最短;
撤去拉力时的速度为v=at,
撤去拉力后,物体的加速度a2=gsinθ+μgcosθ=12m/s2;
设F作用时间为t′,则有: ![]() at′2+
at′2+ ![]() =11
=11
解得:t′= ![]() ≈1.66s
≈1.66s
答:该力作用的最短时间是1.66s
【解析】(1)物体匀速下滑时根据平衡条件求解动摩擦因数;物体沿斜面上升时,根据牛顿第二定律求解加速度大小,再根据位移时间关系求解时间;(2)当物体到达顶端速度恰好为零时,F的作用时间最短,根据牛顿第二定律求出撤去拉力后物体的加速度,再根据位移关系求解时间.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
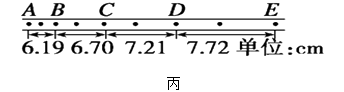
小博士期末闯关100分系列答案【题目】一质点在x轴上运动,它在连续第n秒末所对应的坐标记录在如下表格中,则下列说法正确的是( )
t/s | 0 | 1 | 2 | 3 | 4 | 5 |
x/m | 0 | 5 | -4 | -3 | -8 | 2 |
A.第4s内的位移大小最大
B.第2s内的路程最大
C.前3s内的路程为2m
D.第5s内的位移大小最大