题目内容
7.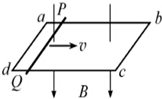 如图,由某种粗细均匀的总电阻为3R的金属条制成的矩形线框abcd,固定在水平面内且处于方向竖直向下的匀强磁场B中.一接入电路电阻为R的导体棒PQ,在水平拉力作用下沿ab、dc以速度v匀速滑动,滑动过程PQ始终与ab垂直,且与线框接触良好,不计摩擦.在PQ从靠近ad处向bc滑动的过程中( )
如图,由某种粗细均匀的总电阻为3R的金属条制成的矩形线框abcd,固定在水平面内且处于方向竖直向下的匀强磁场B中.一接入电路电阻为R的导体棒PQ,在水平拉力作用下沿ab、dc以速度v匀速滑动,滑动过程PQ始终与ab垂直,且与线框接触良好,不计摩擦.在PQ从靠近ad处向bc滑动的过程中( )| A. | PQ中电流先增大后减小 | B. | PQ两端电压先减小后增大 | ||
| C. | PQ上拉力的功率先减小后增大 | D. | 线框消耗的电功率先减小后增大 |
分析 本题分段过程分析:当PQ从左端滑到ab中点的过程和从ab中点滑到右端的过程,抓住PQ产生的感应电动势不变.
导体棒由靠近ab边向dc边匀速滑动的过程中,产生的感应电动势不变,外电路总电阻先增大后减小,由欧姆定律分析PQ两端的电压如何变化;
由题意,PQ上外力的功率等于电功率,由P=$\frac{{E}^{2}}{R}$,分析功率的变化;
当PQ从左端滑到ab中点的过程中,由于总电阻增大,则干路电流减小,PQcb回路的电阻减小,通过cb的电流增大,可知ab中电流减小;当PQ从ab中点滑到右端的过程中,干路电流增大,PQda回路的电阻增大,PQ两端的电压减小,可知ab中电流减小;
根据矩形线框总电阻与PQ电阻的关系,分析其功率如何变化.当矩形线框的总电阻等于PQ的电阻时,线框的功率最大.
解答 解:根据右手定则可知,PQ中电流的方向为Q→P,画出该电路的等效电路图如图,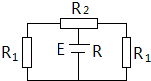
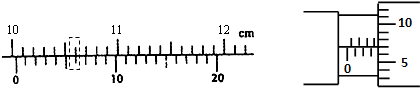
其中R1为ad和bc上的电阻值,R2为ab上的电阻与cd上的电阻的和,电阻之间的关系满足:R1+R2+R1=3R,由题图可知,${R}_{1}=\frac{1}{4}×3R=\frac{3}{4}R$
当导体棒向右运动的过程中,开始时的电阻值:${R}_{0}=\frac{{R}_{1}×({R}_{1}+{R}_{2})}{{R}_{1}+({R}_{1}+{R}_{2})}=\frac{9}{16}R$
当导体棒位于中间位置时,左右两侧的电阻值是相等的,此时:${R}_{中}=\frac{\frac{3R}{2}•\frac{3R}{2}}{\frac{3R}{2}+\frac{3R}{2}}=\frac{3}{4}R>\frac{9}{16}R$,
可知当导体棒向右运动的过程中,开始时的电阻值小于中间位置处的电阻值,所以当导体棒向右运动的过程中电路中的总电阻先增大后减小.
A、导体棒由靠近ad边向bc边匀速滑动的过程中,产生的感应电动势E=BLv,保持不变,外电路总电阻先增大后减小,由欧姆定律分析得知电路中的总电流先减小后增大,即PQ中电流先减小后增大.故A错误.
B、PQ中电流先减小后增大,PQ两端电压为路端电压,U=E-IR,可知PQ两端的电压先增大后减小.故B错误;
C、导体棒匀速运动,PQ上外力的功率等于回路的电功率,而回路的总电阻R先增大后减小,由P=$\frac{{E}^{2}}{R}$得知,PQ上外力的功率先减小后增大.故C正确.
D、由以上的分析可知,导体棒PQ上的电阻始终大于线框的电阻,当导体棒向右运动的过程中电路中的总电阻先增大后减小,根据闭合电路的功率的分配关系与外电阻的关系可知,当外电路的电阻值与电源的内电阻相等时外电路消耗的电功率最大,所以可得线框消耗的电功率先增大后减小.故D错误.
故选:C.
点评 本题一要分析清楚线框总电阻如何变化,抓住PQ位于ad中点时线框总电阻最大,分析电压的变化和电流的变化;二要根据推论:外电阻等于电源的内阻时电源的输出功率最大,分析功率的变化.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案 如图示是α粒子(氦原子核)被重金属原子核散射的运动轨迹,M、N、P、Q是轨迹上的四点,在散射过程中可以认为重金属原子核静止不动.图中所标出的α粒子在各点处的加速度方向正确的是( )
如图示是α粒子(氦原子核)被重金属原子核散射的运动轨迹,M、N、P、Q是轨迹上的四点,在散射过程中可以认为重金属原子核静止不动.图中所标出的α粒子在各点处的加速度方向正确的是( )| A. | M点 | B. | N点 | C. | P点 | D. | Q点 |
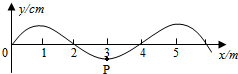 一列沿x轴正方向传播的简谐横波在t=0时刻的波形如图所示,质点P的x坐标为3m.已知任意振动质点连续2次经过平衡位置的时间间隔为0.4s.下列说法正确的是( )
一列沿x轴正方向传播的简谐横波在t=0时刻的波形如图所示,质点P的x坐标为3m.已知任意振动质点连续2次经过平衡位置的时间间隔为0.4s.下列说法正确的是( )| A. | 波速为4m/s | |
| B. | 波的频率为1.25Hz | |
| C. | x坐标为15m的质点在t=0.6s时恰好位于波谷 | |
| D. | x坐标为22m的质点在t=0.2s时恰好位于波峰 | |
| E. | 当质点P位于波峰时,x坐标为17m的质点恰好位于波谷 |
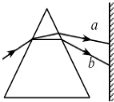 如图,一束光经玻璃三棱镜折射后分为两束单色光a、b,波长分别为λa、λb,该玻璃对单色光a、b的折射率分别为na、nb,则( )
如图,一束光经玻璃三棱镜折射后分为两束单色光a、b,波长分别为λa、λb,该玻璃对单色光a、b的折射率分别为na、nb,则( )| A. | λa<λb,na>nb | B. | λa>λb,na<nb | C. | λa<λb,na<nb | D. | λa>λb,na>nb |
| A. | γ射线是高速运动的电子流 | |
| B. | 氢原子辐射光子后,其绕核运动的电子动能增大 | |
| C. | 太阳辐射能量的主要来源是太阳中发生的重核裂变 | |
| D. | ${\;}_{83}^{210}$Bi的半衰期是5天,100克${\;}_{83}^{210}$Bi经过10天后还剩下50克 |
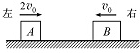 如图,两滑块A、B在光滑水平面上沿同一直线相向运动,滑块A的质量为m,速度大小为2v0,方向向右,滑块B的质量为2m,速度大小为v0,方向向左,两滑块发生弹性碰撞后的运动状态是( )
如图,两滑块A、B在光滑水平面上沿同一直线相向运动,滑块A的质量为m,速度大小为2v0,方向向右,滑块B的质量为2m,速度大小为v0,方向向左,两滑块发生弹性碰撞后的运动状态是( )| A. | A和B都向左运动 | B. | A和B都向右运动 | ||
| C. | A静止,B向右运动 | D. | A向左运动,B向右运动 |
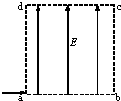 如图所示,长为L(L=ab=dc)高为H(H=bc=ad)的矩形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计重力.
如图所示,长为L(L=ab=dc)高为H(H=bc=ad)的矩形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计重力.