题目内容
16.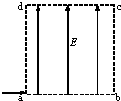 如图所示,长为L(L=ab=dc)高为H(H=bc=ad)的矩形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计重力.
如图所示,长为L(L=ab=dc)高为H(H=bc=ad)的矩形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计重力.(1)若粒子从c点离开电场,求电场强度的大小E和粒子离开电场时的动能Ekt;
(2)若粒子从bc边离开电场时动能为E′k,则电场强度E1为多大?
分析 (1)电荷做类似平抛运动,根据类似平抛运动的分位移公式列式求解电场强度,然后结合动能定理即可求出离开时的动能;
(2)粒子从BC边离开电场,结合在电场方向的偏移,根据动能定理求出电场强度的大小.
解答 解:(1)带电在匀强电场中做类平抛运动,根据分运动公式,有:
L=v0t
H=$\frac{1}{2}a{t}^{2}$
a=$\frac{qE}{m}$
联立解得:E=$\frac{2m{v}_{0}^{2}H}{q{L}^{2}}=\frac{4{E}_{k}H}{q{L}^{2}}$
粒子在电场中运动的过程电场力做功,由动能定理得:qEH=Ekt-Ek
得:Ekt=Ek+qEH=$\frac{4{E}_{k}{H}^{2}}{{L}^{2}}+{E}_{k}$
(2)设粒子从BC边离开电场的偏转量为y′,
则偏转量:$y′=\frac{1}{2}a′t=\frac{1}{2}•\frac{q{E}_{1}{L}^{2}}{m{v}_{0}^{2}}$
根据动能定理得:qE1y′=Ek′-Ek
解得:${E}_{1}=\frac{\sqrt{4{E}_{k}({E}_{k}′-{E}_{k})}}{qL}$
答:(1)若粒子从c点离开电场,电场强度的大小E和粒子离开电场时的动能是$\frac{4{E}_{k}{H}^{2}}{{L}^{2}}+{E}_{k}$;
(2)若粒子从bc边离开电场时动能为E′k,则电场强度E1为$\frac{\sqrt{4{E}_{k}({E}_{k}′-{E}_{k})}}{qL}$.
点评 本题考查了粒子在匀强电场的运动,关键是结合类似平抛运动的分运动公式和牛顿第二定律列式求解,常规题目.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
7.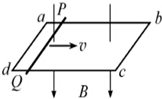 如图,由某种粗细均匀的总电阻为3R的金属条制成的矩形线框abcd,固定在水平面内且处于方向竖直向下的匀强磁场B中.一接入电路电阻为R的导体棒PQ,在水平拉力作用下沿ab、dc以速度v匀速滑动,滑动过程PQ始终与ab垂直,且与线框接触良好,不计摩擦.在PQ从靠近ad处向bc滑动的过程中( )
如图,由某种粗细均匀的总电阻为3R的金属条制成的矩形线框abcd,固定在水平面内且处于方向竖直向下的匀强磁场B中.一接入电路电阻为R的导体棒PQ,在水平拉力作用下沿ab、dc以速度v匀速滑动,滑动过程PQ始终与ab垂直,且与线框接触良好,不计摩擦.在PQ从靠近ad处向bc滑动的过程中( )
 如图,由某种粗细均匀的总电阻为3R的金属条制成的矩形线框abcd,固定在水平面内且处于方向竖直向下的匀强磁场B中.一接入电路电阻为R的导体棒PQ,在水平拉力作用下沿ab、dc以速度v匀速滑动,滑动过程PQ始终与ab垂直,且与线框接触良好,不计摩擦.在PQ从靠近ad处向bc滑动的过程中( )
如图,由某种粗细均匀的总电阻为3R的金属条制成的矩形线框abcd,固定在水平面内且处于方向竖直向下的匀强磁场B中.一接入电路电阻为R的导体棒PQ,在水平拉力作用下沿ab、dc以速度v匀速滑动,滑动过程PQ始终与ab垂直,且与线框接触良好,不计摩擦.在PQ从靠近ad处向bc滑动的过程中( )| A. | PQ中电流先增大后减小 | B. | PQ两端电压先减小后增大 | ||
| C. | PQ上拉力的功率先减小后增大 | D. | 线框消耗的电功率先减小后增大 |
4.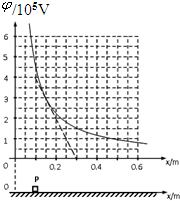 如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,在x轴上的电势φ与坐标x的关系用图中曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视作质点),从x=0.10m处由静止释放,其与水平面的动摩擦因数为0.02.取重力加速度g=10m/s2.则下列说法中不正确的是( )
如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,在x轴上的电势φ与坐标x的关系用图中曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视作质点),从x=0.10m处由静止释放,其与水平面的动摩擦因数为0.02.取重力加速度g=10m/s2.则下列说法中不正确的是( )
 如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,在x轴上的电势φ与坐标x的关系用图中曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视作质点),从x=0.10m处由静止释放,其与水平面的动摩擦因数为0.02.取重力加速度g=10m/s2.则下列说法中不正确的是( )
如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,在x轴上的电势φ与坐标x的关系用图中曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视作质点),从x=0.10m处由静止释放,其与水平面的动摩擦因数为0.02.取重力加速度g=10m/s2.则下列说法中不正确的是( )| A. | 滑块运动的加速度逐渐减小 | |
| B. | 滑块运动的速度先增大后减小 | |
| C. | x=0.15m处的场强大小为2.0×106N/C | |
| D. | 滑块运动的最大速度约为0.1m/s |
1.下列仪器不是利用涡流工作的有( )
| A. | 电磁炉 | B. | 微波炉 | C. | 金属探测器 | D. | 真空冶炼炉 |
5.下列关于光电效应的说法中,不正确的是( )
| A. | 爱因斯坦光电效应方程是:$\frac{1}{2}$mvm2=hν-W | |
| B. | 只要光照射的时间足够长,任何金属都能产生光电效应 | |
| C. | 无论光强多强,只要光的频率小于金属的极限频率就不能产生光电效应 | |
| D. | 发生光电效应时,入射光频率越大所产生的光电子的最大初动能就越大 |
 如图所示,直径分别为D和2D的同心圆处于同一竖直面内,O为圆心,GH为大圆的水平直径.两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场.间距为d的两平行金属极板间有一匀强电场,上级板开有一小孔.一质量为m,电量为+q的粒子由小孔下方$\frac{d}{2}$处静止释放,加速后粒子以竖直向上的速度v射出电场,由H点紧靠大圆内侧射入磁场.不计粒子的重力.
如图所示,直径分别为D和2D的同心圆处于同一竖直面内,O为圆心,GH为大圆的水平直径.两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场.间距为d的两平行金属极板间有一匀强电场,上级板开有一小孔.一质量为m,电量为+q的粒子由小孔下方$\frac{d}{2}$处静止释放,加速后粒子以竖直向上的速度v射出电场,由H点紧靠大圆内侧射入磁场.不计粒子的重力.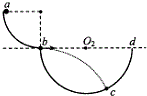 如图所示,半径为r1=1.8m的$\frac{1}{4}$光滑圆弧轨道末端水平,固定在水平地面上,与竖直截面为半圆形的坑平滑连接,bd为坑沿水平方向的直径.现将质量为m=1.0kg的小球从圆弧顶端a点由静止释放,小球离开b点后击中坑壁上的c点.测得c点与水平地面的竖直距离为h=1.8m,重力加速度g取10m/s2.求:
如图所示,半径为r1=1.8m的$\frac{1}{4}$光滑圆弧轨道末端水平,固定在水平地面上,与竖直截面为半圆形的坑平滑连接,bd为坑沿水平方向的直径.现将质量为m=1.0kg的小球从圆弧顶端a点由静止释放,小球离开b点后击中坑壁上的c点.测得c点与水平地面的竖直距离为h=1.8m,重力加速度g取10m/s2.求: 如图所示,竖直平面内有一四分之一光滑圆弧轨道固定在水平桌面AB上,轨道半径R=1.8m,末端与桌面相切于A点,倾角θ=37°的斜面BC紧靠桌面边缘固定,从圆弧轨道最高点由静止释放一个质量m=1kg的可视为质点的滑块a,当a运动到B点时,与a质量相同的另一可视为质点的滑块b从斜面底端C点以初速度v0=5m/s沿斜面向上运动,b运动到斜面上的P点时,a恰好平抛至该点,已知AB的长度x=4m,a与AB间的动摩擦因数μ1=0.25,b与BC间的动摩擦因数μ2=0.5,取g=10m/s2,sin37°=0.6,cos37°=0.8,求
如图所示,竖直平面内有一四分之一光滑圆弧轨道固定在水平桌面AB上,轨道半径R=1.8m,末端与桌面相切于A点,倾角θ=37°的斜面BC紧靠桌面边缘固定,从圆弧轨道最高点由静止释放一个质量m=1kg的可视为质点的滑块a,当a运动到B点时,与a质量相同的另一可视为质点的滑块b从斜面底端C点以初速度v0=5m/s沿斜面向上运动,b运动到斜面上的P点时,a恰好平抛至该点,已知AB的长度x=4m,a与AB间的动摩擦因数μ1=0.25,b与BC间的动摩擦因数μ2=0.5,取g=10m/s2,sin37°=0.6,cos37°=0.8,求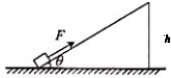 如图所示,质量为m的物体在恒力F的作用下在底端匀速沿斜面向上一直运动到顶端,斜面高h,倾斜角为θ,现把物体放在顶端,发现物体在轻微扰动后可匀速下滑,则在上升过程中恒力F做的功是( )
如图所示,质量为m的物体在恒力F的作用下在底端匀速沿斜面向上一直运动到顶端,斜面高h,倾斜角为θ,现把物体放在顶端,发现物体在轻微扰动后可匀速下滑,则在上升过程中恒力F做的功是( )