题目内容
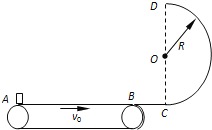
【题目】如图，在竖直平面内，滑道ABC关于B点对称，且A、B、C三点在同一水平线上。先让小滑块以一定的初速度由A沿着滑道滑到C，经过B点和C点的速率各为vB1、v1．再让小滑块以大小相同的初速度由C沿着滑道滑到A，经过B点和A点的速率各为vB2、v2，小滑块与滑道的动摩擦因数恒定，则
A. vB1 > vB2 B. vB1 < vB2 C. v1 > v2 D. v1 = v2
【答案】AC
【解析】试题分析：滑块做圆周运动，根据牛顿第二定律判断滑块受到的支持力大小关系，然后判断摩擦力大小关系，再比较滑块的运动时间，根据动能定理比较速度的大小。
在AB段，由牛顿第二定律得
，滑块受到的支持力
，则速度v越大，滑块受支持力F越小，摩擦力
越小；在BC段，由牛顿第二定律得
，滑块受到的支持力
，则速度v越大，滑块受支持力F越大，摩擦力越大；滑块从A运动到B与从C运动到B的两个过程相比较，A到B的过程中，在AB段滑块所受的摩擦力较小，克服摩擦力做功较少，在BC段摩擦力较大，克服摩擦力做功较多，由动能定理可知
，A正确B错误；从A到C的过程和C到A的过程，通过同一点，在AB段，由牛顿第二定律知，径向的合力提供向心力，从A到B时速度较大，则支持力较小，摩擦力较小，在BC段，径向的合力提供向心力，从A到B，在BC段的速度较小，支持力较小，摩擦力较小，结合动能定理知，从A到C过程中克服摩擦力做功小于从C到A过程中克服摩擦力做功，知
，C正确D错误．
练习册系列答案
阅读快车系列答案
相关题目
