题目内容
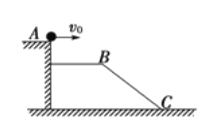
【题目】如图，光滑水平面AB和粗糙斜面BC平滑连接，斜面倾角为53°,AB=BC=3.75m。质量为m=2kg，带电量为
的小物块在与水平面成53°角斜向右上方的强电场中，电场强度为
从A点由静止开始沿ABC运动到C点(取
)，求:
(1)物块从A点运动到B点所用的时间；
(2)若物块在AB和BC上运动的时间之比为2:1，求物块与斜面间的动摩擦因数；
(3)若斜面光滑，改变场强E的大小(方向不变)，仍能使物体沿ABC运动到C，求场强E的取值范围。
【答案】(1) 
；(2) 
；(3)
【解析】
根据牛顿第二定律求得加速度，有运动学公式求得时间；根据运动学公式判断出物体在斜面上运动，利用牛顿第二定律求得摩擦因数；物体能沿AB运动到C，故在AB段
竖直方向的分力最大等于mg即可判断出最大值，当最小时，物体恰能到达C点，即可判断出最小值；根据
E的取值范围；
(1)对物块受力分析，
其中
代入数值解得得
根据位移时间公式可知：
(2)物块在BC上的运动时间
因为
物体在B点的速度为
联立解得
，即物块在斜面上匀速运动
在斜面上
联立上式计算得物块与斜面间的动摩擦因数
(3)当物块与水平地面间弹力恰好为零时，值最大，
此时，
代入数据得
场强E的大小
当物块恰好能到达C点(vC=0)时，值最小
此时，物块在AB间的加速度
span>与BC间的加速度
大小相等
根据牛顿第二定律得
因此有
代入数据计算得
场强E的大小
综上场强E的取值范围为
练习册系列答案
相关题目
