题目内容
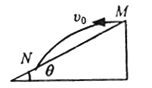
【题目】如图所示，质量m=1kg的小滑块，轻质弹簧的一端与滑块相连，弹簧的另一端固定在挡板上，光滑斜面和光滑圆筒形轨道平滑连接，开始时弹簧处于压缩状态，滑块和小球均处于锁定状态，圆弧的轨道半径R和斜面的顶端C离地面的高度均为1m，斜面与水平面夹角θ=60°，现将滑块解除锁定，滑块运动到C点与小球M相碰时弹簧刚好恢复原长，相碰瞬间小球的锁定被解除，碰后滑块和小球以大小相等的速度向相反的方向运动，碰后小球沿光滑圆筒轨道运动到最高点D水平抛出时对圆筒壁刚好无压力，若滑块与小球碰撞过程时间极短且碰撞过程没有能量损失．g=10m／s2求：
(1)小球从D点抛出后运动的水平距离；
(2)小球的质量；
(3)已知弹簧的弹性势能表达式为EP=
k△x2为弹簧的劲度系数，△x为弹簧的形变量)，求滑块碰后返回过程中滑块的最大动能．
【答案】（1）
（2）
（3）
【解析】（1）小球在D点做平抛运动，设小球的质量为M，则：x1=vDt
联立解得： 
（2）滑块与小球相碰时动量守恒，机械能守恒：
小球从C点到D点的过程中机械能守恒： 
联立解得： 
M=3m=3kg
（3）滑块由B到C过程，弹簧和滑块组成的系统机械能守恒
设碰后滑块距C点距离为x2时动能最大
mgsin600=kx2
滑块返回过程中弹簧和滑块组成的系统的机械能守恒；
联立解得：Ek≈10.14J
练习册系列答案
优等生题库系列答案
相关题目
