Question

【题目】如图所示，一质量Ｍ＝2ｋｇ的长木板Ｂ静止于光滑水平面上，Ｂ的右边放有竖直挡板．现有一小物体Ａ（可视为质点）质量ｍ＝1ｋｇ，以速度ｖ０＝6ｍ／ｓ从Ｂ的左端水平滑上Ｂ，已知Ａ和Ｂ间的动摩擦因数μ＝0．2，Ｂ与竖直挡板的碰撞时间极短，且碰撞时无机械能损失．

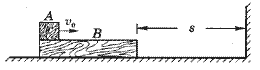
（1）若Ｂ的右端距挡板ｓ＝4ｍ，要使Ａ最终不脱离Ｂ，则木板Ｂ的长度至少多长?
（2）若Ｂ的右端距挡板ｓ＝0．5ｍ，要使Ａ最终不脱离Ｂ，则木板Ｂ的长度至少多长?

Answer 1

【答案】（1）8．67ｍ（2）8．96ｍ．

【解析】（1）设Ａ滑上Ｂ后达到共同速度前并未碰到档板，则根据动量守恒定律得它们的共同速度为ｖ，有ｍｖ０＝（Ｍ＋ｍ）ｖ，

解得ｖ＝2ｍ／ｓ，

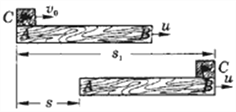
在这一过程中，Ｂ的位移为ｓＢ＝ｖＢ2／2ａＢ且ａＢ＝μｍｇ／Ｍ，

解得ｓＢ＝Ｍｖ2／2μｍｇ＝2×22／2×0．2×1×10＝2ｍ．

设这一过程中，Ａ、Ｂ的相对位移为ｓ１，根据系统的动能定理，得

μｍｇｓ１＝ｍｖ０2－（Ｍ＋ｍ）ｖ2，

解得ｓ１＝6ｍ．

当ｓ＝4ｍ时，Ａ、Ｂ达到共同速度ｖ＝2ｍ／ｓ

后再匀速向前运动2ｍ碰到挡板，Ｂ碰到竖直挡板后，根据动量守恒定律得Ａ、Ｂ最后相对静止时的速度为ｖ′，则Ｍｖ－ｍｖ＝（Ｍ＋ｍ）ｖ′，

解得ｖ′＝ｍ／ｓ．

在这一过程中，Ａ、Ｂ的相对位移为ｓ２，根据系统的动能定理，得

μｍｇｓ２＝（Ｍ＋ｍ）ｖ2－（Ｍ＋ｍ）ｖ′2，

解得ｓ２＝2．67ｍ．

因此，Ａ、Ｂ最终不脱离的木板最小长度为ｓ１＋ｓ２＝8．67ｍ

（2）因Ｂ离竖直档板的距离ｓ＝0．5ｍ＜2ｍ，所以碰到档板时，Ａ、Ｂ未达到相对静止，此时Ｂ的速度ｖＢ为

ｖＢ2＝2ａＢｓ＝2ｓ，

解得ｖＢ＝1ｍ／ｓ，

设此时Ａ的速度为ｖＡ，根据动量守恒定律，得ｍｖ０＝ＭｖＢ＋ｍｖＡ，

解得ｖＡ＝4ｍ／ｓ，

设在这一过程中，Ａ、Ｂ发生的相对位移为ｓ１′，根据动能定理得：

μｍｇｓ１′＝ｍｖ０2－（ｍｖＡ2＋ＭｖＢ2），

解得ｓ１′＝4.5ｍ．

Ｂ碰撞挡板后，Ａ、Ｂ最终达到向右的相同速度ｖ，根据动量守恒得ｍｖＡ－ＭｖＢ＝（Ｍ＋ｍ）ｖ，

解得ｖ＝ｍ／ｓ．

在这一过程中，Ａ、Ｂ发生的相对位移ｓ２′为

μｍｇｓ２′＝ｍｖＡ2＋（Ｍ＋ｍ）ｖ2，

解得ｓ２′＝ｍ．

Ｂ再次碰到挡板后，Ａ、Ｂ最终以相同的速度ｖ′向左共同运动，根据动量守恒定律，得

Ｍｖ－ｍｖ＝（Ｍ＋ｍ）ｖ′，

解得ｖ′＝ｍ／ｓ．

在这一过程中，Ａ、Ｂ发生的相对位移ｓ３′为：

μｍｇｓ３′＝（Ｍ＋ｍ）ｖ2－（Ｍ＋ｍ）ｖ′2，

解得ｓ３′＝ｍ．

因此，为使Ａ不从Ｂ上脱落，Ｂ的最小长度为ｓ１′＋ｓ２′＋ｓ３′＝8.96ｍ．