题目内容
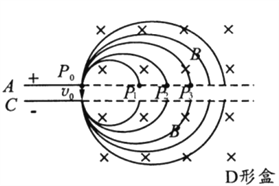
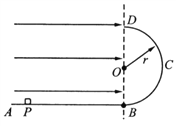
【题目】如图,固定在竖直面内的光滑绝缘轨道由水平段AB和半径为r的半圆环段BCD平滑相切而成,过圆环直径BOD的虚线左侧存在方向水平向右的匀强电场。现将一可视为质点的带正电小滑块,从水平轨道上的P点由静止释放,滑块沿轨道运动到半圆环上B点时对轨道的压力等于滑块重力的7倍,且滑块离开半圆环后不经任何碰撞回到了B点。关于上述过程,下列说法正确的是( )
A. 滑块不能沿轨道运动到最高点D
B. 滑块两次经过B点时的速度相同
C. 在虚线左侧,滑块到达距水平轨道高为![]() 的位置时,电场力的瞬时功率为零
的位置时,电场力的瞬时功率为零
D. P到B点的距离为![]()
【答案】CD
【解析】A、第一次经过B点有![]() ,解得
,解得![]() ,从B到D有动能定理可得
,从B到D有动能定理可得![]() ,解得
,解得![]() ,所以滑块能沿轨道运动到最高点D,故A错误;
,所以滑块能沿轨道运动到最高点D,故A错误;
B、从D飞出做匀变速曲线运动,竖直方向做自由落体运动,水平方向做匀减速运动,滑块从D回到B点过程,电场力不做功,只有重力做功,所以滑块两次经过B点时的速度大小相同,方向不同,故B错误;
C、在虚线左侧,滑块到达距水平轨道高为![]() 的位置时,运动时间为
的位置时,运动时间为![]() ,从滑块到达距水平轨道高为
,从滑块到达距水平轨道高为![]() 的位置运动到B的时间为
的位置运动到B的时间为![]() ,则有
,则有![]() ,根据运动的对称性可知,滑块到达距水平轨道高为
,根据运动的对称性可知,滑块到达距水平轨道高为![]() 的位置时水平方向的速度为0,所以电场力的瞬时功率为零,故C正确;
的位置时水平方向的速度为0,所以电场力的瞬时功率为零,故C正确;
D、由题意可解得![]() ,所以电场力的大小为
,所以电场力的大小为![]() ,从P到B点由动能定理可得
,从P到B点由动能定理可得![]() ,解得P到B点的距离为
,解得P到B点的距离为![]() ,故D正确;
,故D正确;
故选CD。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目