Question

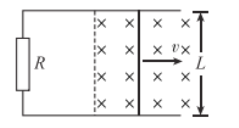
【题目】宇航员在某星球表面做了如下实验用于测量星球表面的重力加速度:将小球从空中的某一高度由静止释放，下落过程小球由于受到空气阻力作用做变加速运动，测得加速度随速度的变化图象如图所示，假设小球落地前已开始做匀速直线运动。已知图中直线在纵轴与横轴的截距分别为a0、v0，小球的质量为m，星球的半径为R，万有引力常量为G，忽略星球自转的影响，由上述条件可判断出

A.该星球表面的重力加速度为a0

B.空气阻力与速率平方成正比

C.该星球的平均密度为ρ=

D.该星球的第一宇宙速度为

Answer 1

【答案】AD

【解析】

AB．小球下落过程受重力、空气阻力作用，根据牛顿运动定律和图象形状得

ma =mg-kv，

空气阻力满足f=kv；由图象可知，当v=0时a=a0，即mg =ma0，则g=a0，A正确，B错误；

C．星球表面附近重力约等于万有引力，即

mg =G，

联立星球密度公式

ρ=，

得

ρ=，

C错误；

D．星球的第一宇宙速度为卫星环绕的最大速度，由万有引力提供向心力

G=m

联立

mg=G

得

v=

D正确。