题目内容
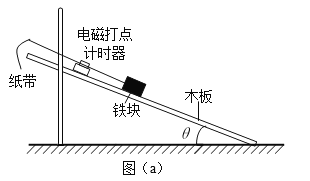
【题目】如图所示，一对光滑的、间距为L=10cm的金属导轨，AB、DE段水平，BC、EF段圆形导轨的半径R=0. 5m，在BE处分别与AB、DE相切，BE与导轨垂直，导轨电阻不计。在导轨的AD端接有一个电动势E=6V、内阻r=0. 2
的电源和一个R2=2. 6的电阻。导轨间存在着垂直于导体棒方向的匀强磁场（图中未画出）。一质量为m=0. 012kg、电阻为R1=0. 2的金属棒MN放在圆形导轨上，MN的方向与导轨垂直，通电后能恰能静止在圆导轨上，且与BE的水平距离为x=0. 3m。求：
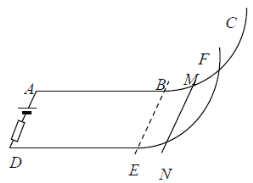
(1)若磁场沿竖直方向，是竖直向上还是竖直向下？磁感应强度多大？
(2)若磁场的方向可变，磁感应强度最小值多大？
【答案】(1)竖直向下 0.45T (2)0.36T
【解析】
(1)若磁场沿竖直方向，则金属棒MN受到的安培力是水平方向，金属棒MN能静止在圆导轨上，则安培力的方向水平向右，金属棒MN中电流方向为
，据左手定则可得，磁场方向竖直向下．
对金属棒MN受力分析如图，则：
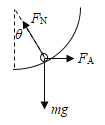
由几何关系得
由三力平衡得
由闭合电路欧姆定律得
代入数据解得
(2)当物体所受安培力的方向沿轨道切线向上时，安培力最小，磁感应强度最小，对应的磁场方向如图：
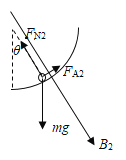
由平衡条件可得
解得：磁感应强度的最小值
练习册系列答案
相关题目
