题目内容
如图所示,间距为l的两条足够长的平行金属导轨与水平面的夹角为![]() ,导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2,两根质量均为m、有效电阻均匀为R的导体棒a和b放在导轨上,并与导轨垂直.(设重力加速度为g)
,导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2,两根质量均为m、有效电阻均匀为R的导体棒a和b放在导轨上,并与导轨垂直.(设重力加速度为g)

(1)若a进入第2个磁场区域时,b以与a同样的速度进入第1个磁场区域,求b穿过第1个磁场区域过程中增加的动能![]() .
.
(2)若a进入第2个磁场区域时,b恰好离开第1个磁场区域;此后a离开第2个磁场区域时,b又恰好进入第2个磁场区域.且a、b在任意一个磁场区域或无磁场区域的运动时间均相等.求a穿过第2个磁场区域过程中,两导体棒产生的总焦耳热Q.
(3)对于第(2)问所述的运动情况,求a穿出第k个磁场区域时的速率v.
(1)mgd1sinθ (2)mg(d1+d2)sinθ (3) ![]() -
-![]()
解析:(1)a和b不受安培力的作用,由机械能守恒知
ΔEk=mgd1sinθ. ①
(2)设导体棒刚进入无磁场区域时的速度为v1,刚离开无磁场区域时的速度为v2,由能量守恒知
在磁场区域中![]() mv12+Q=
mv12+Q=![]() mv22+mgd1sinθ ②
mv22+mgd1sinθ ②
在无磁场区域中![]() mv22=
mv22=![]() mv12+mgd2sinθ ③
mv12+mgd2sinθ ③
解得Q=mg(d1+d2)sinθ. ④
(3)在无磁场区域,根据匀变速直线运动规律
v2-v1=gtsinθ ⑤
且平均速度![]() ⑥
⑥
有磁场区域,棒a受到合力F=mgsinθ-BIl ⑦
感应电动势E=Blv ⑧
感应电流I=![]() ⑨
⑨
解得F=mgsinθ-![]() ⑩
⑩
根据牛顿第二定律,在t到t+Δt时间内
∑Δv=∑![]() Δt
Δt ![]()
则有∑Δv=∑[gsinθ-![]() ]Δt
]Δt ![]()
解得v1-v2=gtsinθ-![]() D.1.
D.1. ![]()
联立⑤⑥![]() 式,解得
式,解得
v1=![]()
由题意知,
v=v1=![]() .
.

 如图所示,间距为L的光滑平行金属导轨,水平地放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻.一电阻是R0,质量为m的导体棒放置在导轨上,在外力F作用下从t=0的时刻开始运动,不计导轨电阻,
如图所示,间距为L的光滑平行金属导轨,水平地放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻.一电阻是R0,质量为m的导体棒放置在导轨上,在外力F作用下从t=0的时刻开始运动,不计导轨电阻,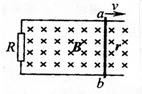 (2011?珠海一模)如图所示,间距为L的平行金属导轨上,有一电阻为r的金属棒ab与导轨接触良好.导轨左端连接电阻R,其它电阻不计,磁感应强度为B,金属捧ab以速度v向右作匀速运动,则( )
(2011?珠海一模)如图所示,间距为L的平行金属导轨上,有一电阻为r的金属棒ab与导轨接触良好.导轨左端连接电阻R,其它电阻不计,磁感应强度为B,金属捧ab以速度v向右作匀速运动,则( ) 如图所示,间距为L的两条足够长的平行金属导轨MN,PQ与水平面夹角为a,导轨的电阻不计,导轨的N、P端连接一阻值为R的电阻,导轨置于磁感应强度大小为B、方向与导轨平面垂直的匀强磁场中.将一根质量为m、电阻为r的导体棒垂直放在导轨上,导体棒ab恰能保持静止.现给导体棒一个大小为v0、方向沿导轨平面向下的初速度,然后任其运动,导体棒在运动过程中始终保持与导轨垂直并接触良好.设导体棒所受滑动摩擦力与最大静摩擦力大小相等,求:
如图所示,间距为L的两条足够长的平行金属导轨MN,PQ与水平面夹角为a,导轨的电阻不计,导轨的N、P端连接一阻值为R的电阻,导轨置于磁感应强度大小为B、方向与导轨平面垂直的匀强磁场中.将一根质量为m、电阻为r的导体棒垂直放在导轨上,导体棒ab恰能保持静止.现给导体棒一个大小为v0、方向沿导轨平面向下的初速度,然后任其运动,导体棒在运动过程中始终保持与导轨垂直并接触良好.设导体棒所受滑动摩擦力与最大静摩擦力大小相等,求: 下由静止开始运动,当cd刚要滑动时ab恰达到最大速度.(θ=30、μ=、最大静摩擦力等于滑动摩擦力)求:
下由静止开始运动,当cd刚要滑动时ab恰达到最大速度.(θ=30、μ=、最大静摩擦力等于滑动摩擦力)求: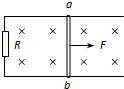 如图所示,间距为L的光滑平行金属导轨水平放置,匀强磁场的磁感应强度为B,方向垂直于导轨平面向下.导轨上有一质量为m、长为L的金属棒ab,金属棒电阻为R,导轨的一端连接阻值也为R的电阻,导轨电阻不计,金属棒ab在一水平恒力F作用下由静止开始向右运动,棒与导轨始终保持良好接触.求:
如图所示,间距为L的光滑平行金属导轨水平放置,匀强磁场的磁感应强度为B,方向垂直于导轨平面向下.导轨上有一质量为m、长为L的金属棒ab,金属棒电阻为R,导轨的一端连接阻值也为R的电阻,导轨电阻不计,金属棒ab在一水平恒力F作用下由静止开始向右运动,棒与导轨始终保持良好接触.求: