题目内容
【题目】如图,真空室内存在匀强磁场,磁场方向垂直于图中纸面向里,磁感应强度的大小B=0.60T,磁场内有一块平面感光平板ab,板面与磁场方向平行,在距ab的距离l =16cm处,有一个点状的放射源S,它向各个方向发射粒子,粒子的速度都是v =3.0×106m/s,已知粒子的电荷与质量之比![]() ,现只考虑在图纸平面中运动的粒子。
,现只考虑在图纸平面中运动的粒子。
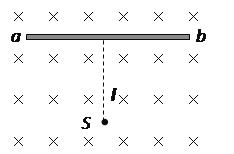
求(1)ab上被粒子打中的区域的长度;
(2)能打在板上的粒子的初速度方向间的最大夹角。
【答案】(1) ![]() (2)
(2) ![]()
【解析】(1)α粒子带正电,故在磁场中沿逆时针方向做匀速圆周运动,用R表示轨道半径,有: ![]()
代入数据得R=10 cm
可见,2R>l>R.
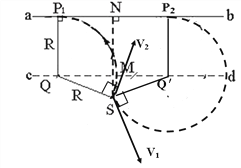
因朝不同方向发射的α粒子的圆轨迹都过S,由此可知,某一圆轨迹在图中N左侧与ab相切,则此切点P1就是α粒子能打中的左侧最远点.为定出P1点的位置,可作平行于ab的直线cd,cd到ab间的距离为R,以S为圆心,R为半径,作弧交cd于Q点,再过Q作ab的垂线交ab于P1.由图中几何关系得:NP1=![]()
再考虑N的右侧.任何α粒子在运动中离S的距离不可能超过2R,以2R为半径,S为圆心作圆,交ab于N点右侧的P2点,此即右侧能打到的最远点.由图中几何关系得

NP2=![]()
所求长度为P1P2=NP1+NP2
代入数值得P1P2=20 cm
(2)如图,沿v1方向射出粒子与屏相切于p1点,沿v2方向射出粒子与屏相切于p2 点v1, v2间夹角为所求最大夹角,此夹角等于分别与之垂直的半径间的夹角,既SQ、SQ′间的夹角
![]() (或
(或![]() )
)
则所求夹角为![]() (或
(或![]() )
)

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目