题目内容
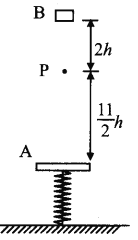
【题目】如图所示，一根被锁定的压缩轻弹簧下端固定在水平地面上，上端固定着一质量为m的薄木板A，弹簧的压缩量为
h。图中P点距地面高度正好等于弹簧原长，在P点上方有一距它高度为2h、质量为2m的物块B。现解除弹簧的锁定，木板A上升到P点时恰好与自由下落的物块B发生正碰(碰撞时间极短)，并一起无粘连地向下运动。B与A第一次分开后能达到的最高位置在P点上方的
处。已知重力加速度为g，整个过程中弹簧始终处于弹性限度内并保持竖直。求：
(1)A、B第一次分开瞬间B的速度大小
(2)A、B第一次碰撞后一起向下运动到A的初始位置时速度的大小。
【答案】(1)
(2)
【解析】（1）B与A刚要分离时，弹簧正好处于原长，设此时B的速度为vB，则由机械能守恒：
解得
（2）设AB刚好碰撞前B的速度大小为v，根据机械能守恒：
根据机械能守恒，AB碰撞后瞬间的速度大小vAB与AB刚好分开时速度大小相等，即：vAB=vB设AB刚好碰撞前A的速度大小为vA，根据动量守恒：
2mv-mvA=3mvAB
解得
设弹簧锁定时的弹性势能为EP，从弹簧解除锁定到恢复到原长的过程，根据机械能守恒定律：
设AB第一次碰撞后一起向下运动到A的初始位置时的速度大小为v′，在这过程中，根据机械能守恒：
以上各式解得：
练习册系列答案
相关题目
