题目内容
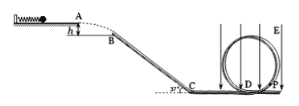
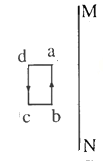
【题目】如图所示,空间中有沿y轴负方向的匀强电场,其中y轴左侧场强为E1,y轴右侧场强为E2,y轴右侧有宽度为d的匀强磁场,方向垂直于纸面向里。图中MN之间固定一绝缘细管,倾角θ=37°,现有一质量为m,电荷量为-q(q>0)的带电小球,从x轴的M点处从静止开始沿细管运动(小球直径比细管略小,可视为质点),从y轴上y=3L的N点进入磁场,此后小球恰好未从右侧穿出磁场区域,已知重力加速度为g,B1=![]() ,B2=
,B2=![]() ,小球与管壁间的动摩擦因数为μ(Sin37°=0.6 cos37°=0.8)求:
,小球与管壁间的动摩擦因数为μ(Sin37°=0.6 cos37°=0.8)求:
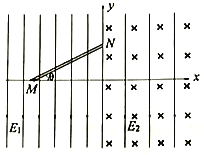
(1)小球从N点进入磁场时速度v的大小;
(2)磁感应强度B的大小。
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)在y轴左侧区域,对小球受力分析,小球所受的重力和电场力的合力可视为等效重力,根据动能定理求解小球从N点进入磁场时速度v的大小;(2)在y轴右侧,由于小球做匀速圆周运动,重力与电场力平衡,由几何关系求解半径,根据![]() 求解B.
求解B.
(1)在y轴左侧区域,对小球受力分析,小球所受的重力和电场力的合力可视为等效重力G′,则有:G′=qE1-mg=0.5mg,
方向竖直向上;由M到N,由动能定理:![]()
解得![]()
(2)在y轴右侧,由于小球做匀速圆周运动,qE2=mg
设半径为R,根据牛顿第二定律:![]()
由几何关系可知:Rsinθ+R=d
联立解得![]()

练习册系列答案
相关题目