ƒøƒ⁄»ð
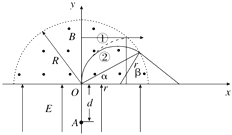
°æƒø°ø»ÁÕºÀ˘ 棨x÷·…œ∑Ω“‘‘≠µ„OŒ™‘≤–ƒ°¢∞Îæ∂Œ™Rµƒ∞Α≤–Œ«¯”Úƒ⁄¥Ê‘⁄‘»«ø¥≈≥°£¨¥≈≥°µƒ∑ΩœÚ¥π÷±”⁄xy∆Ω√Ê≤¢÷∏œÚ÷Ω√ÊÕ‚£¨¥≈∏–”¶«ø∂»Œ™B£Æ‘⁄x÷·£®©ÅR£¨R£©œ¬∑Ωµƒ«¯”Úƒ⁄¥Ê‘⁄∑ΩœÚ”Îy÷·œýÕ¨µƒ‘»«øµÁ≥°£Æy÷·œ¬∑ΩµƒAµ„”ÎOµ„µƒæý¿ÎŒ™d£¨“ª÷ ¡øŒ™m°¢µÁ∫…¡øŒ™qµƒ¥¯’˝µÁ¡£◊”¥”Aµ„”…æ≤÷π Õ∑≈£¨æ≠µÁ≥°º”ÀŸ∫Û¥”Oµ„…‰»Î¥≈≥°£¨≤ªº∆¡£◊”µƒ÷ÿ¡¶◊˜”√£Æ
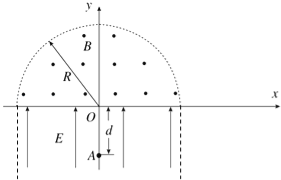
£®1£©“™ π¡£◊”Ω¯»Î¥≈≥°÷Æ∫Û≤ª‘Ÿæ≠π˝x÷·£¨µÁ≥°«ø∂»–Ë¥Û”⁄ªÚµ»”⁄ƒ≥∏ˆ÷µE£¨«ÛE£ª
£®2£©»ÙµÁ≥°«ø∂»±‰ªØŒ™µ⁄£®1£©Œ Eµƒ![]() £¨«Û¡£◊”æ≠π˝¥≈≥°∆´◊™∫ÛµΩ¥Ôx÷· ±µƒ◊¯±Í£ª≤¢«Û¡£◊”¥”Aµ„≥ˆ∑¢µΩ∏√Œª÷√µƒ ±º‰£Æ
£¨«Û¡£◊”æ≠π˝¥≈≥°∆´◊™∫ÛµΩ¥Ôx÷· ±µƒ◊¯±Í£ª≤¢«Û¡£◊”¥”Aµ„≥ˆ∑¢µΩ∏√Œª÷√µƒ ±º‰£Æ
°æ¥∞∏°ø£®1£©“™ π¡£◊”Ω¯»Î¥≈≥°÷Æ∫Û≤ª‘Ÿæ≠π˝x÷·£¨µÁ≥°«ø∂»–Ë¥Û”⁄ªÚµ»”⁄ƒ≥∏ˆ÷µE£¨EŒ™![]() £ª
£ª
£®2£©»ÙµÁ≥°«ø∂»±‰ªØŒ™µ⁄£®1£©Œ Eµƒ![]() £¨«Û¡£◊”æ≠π˝¥≈≥°∆´◊™∫ÛµΩ¥Ôx÷· ±µƒ◊¯±ÍŒ™£∫£®
£¨«Û¡£◊”æ≠π˝¥≈≥°∆´◊™∫ÛµΩ¥Ôx÷· ±µƒ◊¯±ÍŒ™£∫£®![]() R£¨0£©£¨¡£◊”¥”Aµ„≥ˆ∑¢µΩ∏√Œª÷√µƒ ±º‰Œ™£®
R£¨0£©£¨¡£◊”¥”Aµ„≥ˆ∑¢µΩ∏√Œª÷√µƒ ±º‰Œ™£®![]() +
+![]() +
+![]() £©
£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø
‘£®1£©¡£◊”‘⁄µÁ≥°÷–º”ÀŸ£¨‘⁄¥≈≥°÷–◊ˆ‘»ÀŸ‘≤÷БÀ∂Ø£¨”¶”√∂؃Ð∂®¿Ì”Î≈£∂Ÿµ⁄∂˛∂®¬…ø…“‘«Û≥ˆµÁ≥°«ø∂»E£Æ
£®2£©∑÷Œˆ«Â≥˛¡£◊”‘À∂Øπ˝≥㨫Û≥ˆ¡£◊”‘⁄∏˜Ω◊∂Œµƒ‘À∂Ø ±º‰£¨»ª∫Û«Û≥ˆ¡£◊”◊еƒ‘À∂Ø ±º‰£Æ
Ω‚£∫£®1£©¡£◊”‘⁄µÁ≥°÷–º”ÀŸ£¨”…∂؃Ð∂®¿Ìµ√£∫qEd=![]() mv2£¨
mv2£¨
¡£◊”Ω¯»Î¥≈≥°∫Û◊ˆ‘≤÷БÀ∂Ø£¨”…≈£∂Ÿµ⁄∂˛∂®¬…µ√£∫qvB=m![]() £¨
£¨
¡£◊”÷Æ∫Û«°∫√≤ª‘Ÿæ≠π˝x÷·£¨‘Ú¿Îø™¥≈≥° ±µƒÀŸ∂»∑ΩœÚ”Îx÷·∆Ω––£¨‘À∂Ø«Èøˆ»ÁÕº¢ŸÀ˘ 棨
”…º∏∫Œ÷™ ∂µ√£∫R=![]() r£¨
r£¨
Ω‚µ√£∫E=![]() £ª
£ª
£®2£©Ω´E°‰=![]() E¥˙»ÎE=
E¥˙»ÎE=![]() ø…µ√¡£◊”‘⁄¥≈≥°÷–‘À∂صƒπϵ¿∞Îæ∂£∫r=
ø…µ√¡£◊”‘⁄¥≈≥°÷–‘À∂صƒπϵ¿∞Îæ∂£∫r=![]() £¨
£¨
¡£◊”‘À∂Ø«Èøˆ»ÁÕº¢⁄£¨Õº÷–µƒΩ«∂»¶¡°¢¶¬¬˙◊„£∫cos¶¡=![]() =
=![]() £¨
£¨
º¥£∫¶¡=30°„£¨¶¬=2¶¡=60°„£¨
¡£◊”æ≠π˝x÷· ±µƒŒª÷√◊¯±ÍŒ™£∫x=r+![]() £¨
£¨
Ω‚µ√£∫x=![]() R£Æ
R£Æ
¡£◊”‘⁄¥≈≥°÷–µƒÀŸ∂»£∫v=![]() £¨
£¨
µÁ≥°÷–‘À∂Ø ±º‰Œ™£∫t1=![]() £¨
£¨
¥≈≥°÷–‘À∂Ø ±º‰Œ™£∫t2=![]() £¨
£¨
≥ˆ¥≈≥°∫ÛµΩX÷· ±º‰Œ™£∫t3=![]() £¨
£¨
¥”Aµ„≥ˆ∑¢‘À∂صƒ◊Ð ±º‰ «£∫t=t1+t2+t3=£®![]() +
+![]() +
+![]() £©
£©![]() £ª
£ª
¥£∫£®1£©“™ π¡£◊”Ω¯»Î¥≈≥°÷Æ∫Û≤ª‘Ÿæ≠π˝x÷·£¨µÁ≥°«ø∂»–Ë¥Û”⁄ªÚµ»”⁄ƒ≥∏ˆ÷µE£¨EŒ™![]() £ª
£ª
£®2£©»ÙµÁ≥°«ø∂»±‰ªØŒ™µ⁄£®1£©Œ Eµƒ![]() £¨«Û¡£◊”æ≠π˝¥≈≥°∆´◊™∫ÛµΩ¥Ôx÷· ±µƒ◊¯±ÍŒ™£∫£®
£¨«Û¡£◊”æ≠π˝¥≈≥°∆´◊™∫ÛµΩ¥Ôx÷· ±µƒ◊¯±ÍŒ™£∫£®![]() R£¨0£©£¨¡£◊”¥”Aµ„≥ˆ∑¢µΩ∏√Œª÷√µƒ ±º‰Œ™£®
R£¨0£©£¨¡£◊”¥”Aµ„≥ˆ∑¢µΩ∏√Œª÷√µƒ ±º‰Œ™£®![]() +
+![]() +
+![]() £©
£©![]() £Æ
£Æ