��Ŀ����
����Ŀ����ͼ��ʾ��ֱ������ϵxOyλ����ֱƽ���ڣ���ˮƽ��x���·�������ǿ�ų�����ǿ�糡���ų��ĴŸ�ӦΪB������ֱxOyƽ������糡��ƽ����y�ᣮһ����Ϊm�������Ϊq�Ĵ������С��y���ϵ�A��ˮƽ�����׳�����x���ϵ�M�����糡�ʹų���ǡ��������Բ���˶�����x���ϵ�N���һ���뿪�糡�ʹų���MN֮��ľ���ΪL��С���M��ʱ���ٶȷ�����x��ķ���н�Ϊ�ȣ����ƿ����������������ٶ�Ϊg����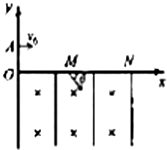
��1���糡ǿ��E�Ĵ�С�ͷ���
��2��С���A���׳�ʱ���ٶ�v0�Ĵ�С��
��3��A�㵽x��ĸ߶�h��
���𰸡�
��1���⣺С���ڵ糡���ų���ǡ��������Բ���˶���
˵���糡��������ƽ�⣨�������ܳ䵱Բ���˶�������������
��qE=mg��
��ã�E= ![]() ��
��
�����ķ�����ֱ���£��糡������ֻ�����ϣ�
����С������磬���Ե糡ǿ�ȷ�����ֱ���ϣ�
�𣺵糡ǿ��E�Ĵ�СΪ�� ![]() ��������ֱ����
��������ֱ����
��2���⣺С��������Բ���˶���O��ΪԲ�ģ�MNΪ�ҳ���
��MO��P=�ȣ���ͼ��ʾ����뾶Ϊr���ɼ��ι�ϵ֪��sin��= ![]() ��
��

С��������Բ���˶��������������������ṩ����С����Բ���˶�������Ϊv��
��ţ�ٵڶ����ɵã�qvB=m ![]() ��
��
���ٶȵĺϳ���ֽ�֪��cos��= ![]() ��
��
��ã�v0= ![]() ��
��
��С���A���׳�ʱ���ٶ�v0�Ĵ�СΪ ![]()
��3���⣺��С��M��ʱ����ֱ���ٶ�Ϊvy��
����ˮƽ���ٶȵĹ�ϵΪ��vy=v0tan�ȣ�
���ȱ���ֱ���˶����ɵã�vy2=2gh��
��ã�h= ![]() ��
��
��A�㵽x��ĸ߶�hΪ ![]()
����������1������С�����ܵ��������糡��������������ͬ������������Բ���˶����ɵ�֪�糡����������һ��ƽ�������Ӷ��ɵ�֪�糡�ķ����ɶ���ƽ�������糡�Ĵ�С����2�����ɼ��ι�ϵ��ʾ��С���ڸ��ϳ�����Բ���˶��İ뾶����ϰ뾶��ʽ���ٶȵķֽ⣬������С���׳�ʱ�ij��ٶȣ���3��С���ڵ糡������ƽ���˶���Ӧ����ƽ���˶����ɿ������h��С��