题目内容
【题目】一足够大的水池内盛有某种透明液体,液体的深度为 ![]() m,在水池底部中央放一点光源S,其中一条光线以30°的入射角射到液体与空气的界面上,它的反射光线与折射光线的夹角为97°(cos37°=0.8)
m,在水池底部中央放一点光源S,其中一条光线以30°的入射角射到液体与空气的界面上,它的反射光线与折射光线的夹角为97°(cos37°=0.8)
求:
(1)这种液体的折射率;
(2)液体表面亮斑的面积.
【答案】
(1)解:已知入射角i=30°,根据反射定律知:反射角 i′=i
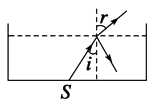
由题有:r+i′=180°﹣97°
解得 r=53°
所以这种液体的折射率 n= ![]() =
= ![]() =1.6
=1.6
答:这种液体的折射率是1.6;
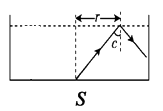
(2)光线在亮斑边缘恰好发生全反射,入射角等于临界角C,则
sinC= ![]() =
= ![]()
则 tanC= ![]() =
= ![]() =
= ![]()
亮斑半径:r=HtanC= ![]() ×
× ![]() m=5m
m=5m
亮斑面积:S=πr2=3.14×52=78.5m2
答:液体表面亮斑的面积是78.5m2.
【解析】(1)首先根据题意画出光路图,结合几何知识求折射角,根据折射定律,求出液体的折射率。
(2)求亮斑的面积,首先要求出亮斑的边缘位置,光线再亮斑的边缘位置发生全反射,是题目中的主要隐含条件。根据折射率和临界角之间的关系求出临界角,再结合几何知识求出亮斑的面积。

【题目】电动自行车是生活中重要的交通工具,某品牌电动自行车的铭牌如下:
车型: | 电池规格: |
20寸(车轮直径:508mm) | 36V12Ah(蓄电池) |
整车质量:40kg | 额定转速:210r/min(转/分) |
外形尺寸: | 充电时间:2h~8h |
电机:后轮驱动、直流永磁式电机 | 额定工作电压/电流:36V/5A |
当蓄电池充满电量后,根据此铭牌中的有关数据,下列说法不正确的是( )
A.该车的额定功率约为4.32×102W
B.该车的额定时速约为20km/h
C.该车约能行驶2.4小时
D.该车一次充满电所储存的电能约为1.56×106J