题目内容
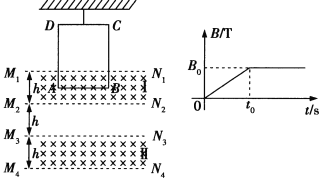
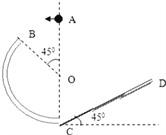
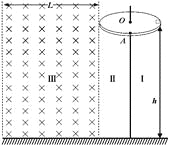
【题目】如图所示，一质量为m=0.5kg，电荷量为q=+0.2C的小物块（可视为质点），放在离地面高度为h=5m的水平放置、厚度不计的绝缘圆盘边缘，并随圆盘一起绕中心转轴顺时针做匀速圆周运动，圆盘的角速度为ω=2rad/s，半径为r=1m，圆盘和小物块之间的动摩擦因数为μ=0.5。以圆盘左侧垂直于纸面的切面和过圆盘圆心O点与空间中A点的竖直平面为界（两平面平行），将空间分为Ⅰ、Ⅱ、Ⅲ三个空间区域，当小物块转动时，Ⅰ区域出现随时间均匀增大的电场E（图中未画出），电场方向是竖直方向。当E增大到E1时，小物块刚好从空间中的A点离开圆盘，且垂直于Ⅰ、Ⅱ区域边界进入Ⅱ区域，此时，Ⅱ区域和Ⅲ区域立即出现一竖直向上的匀强电场E2（图中未画出），E2=25N/C，且Ⅲ区域有一垂直于纸面向里的匀强磁场，磁场宽度为L=4m，g=10m/s2。求：
（1）E1的大小和方向；
（2）若小物块在磁场宽度范围内落地，则磁感应强度B的取值范围是多少？
（3）现将磁感应强度B取某一值，当小物块离开A后一小段时间，紧贴圆盘圆心O点下方以速度v0=
m/s水平抛出一木制小球，最终两者在磁场宽度范围内的地面上相遇，则从小物块离开A点时开始计时，抛出木制小球的时刻t为多少？
【答案】（1）
，竖直向上（2）
（3）
【解析】试题分析：（1）当Ⅰ区域的电场向上时，小物块与圆盘间的最大静摩擦力减小，当其减小到等于向心力时，小物块沿切线方向飞出，所以，
的方向竖直向上．
由牛顿第二定律有：
代入数据解得：
（2）在Ⅱ、Ⅲ区域，由于
，所以小物块先做匀速直线运动，进入Ⅲ区域后，做匀速圆周运动．
设小物块速度为v，圆周运动的半径为Ⅲ，则有：
，
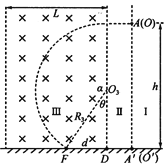
要使其在磁场宽度范围内落地，其轨道如图所示．设半径的极小值和极大值分别为
和
，则有：
联立并代入数据解得：．
（3）设木制小球落地点为F，运动时间为
，水平位移为x，
、
分别为
在地面上的投影，FD的长度为d，则有：
；
由几何知识有：
联立并代入数据解得：
设小物块整个运动的时间为
，在Ⅲ区域的运动半径为
，周期为T，则有：
解得：
，
，代入数据解得：
，又
，代入数据得：
所以小物块做圆周运动转过角度为：
所以：
，则：
，联立解得：
