题目内容
用长L=1.6m的细绳,一端系着质量M=1kg的木块,另一端挂在固定点上。现有一颗质量m=20g的子弹以v1=500m/s的水平速度向木块中心射击,结果子弹穿出木块后以v2=100m/s的速度前进。问木块能运动到多高?(取g=10m/s2,空气阻力不计)
2.96m
【错解分析】错解:在水平方向动量守恒,有
mv1=Mv+mv2 (1)
式①中v为木块被子弹击中后的速度。木块被子弹击中后便以速度v开始摆动。由于绳子对木块的拉力跟木块的位移垂直,对木块不做功,所以木块的机械能守恒,即
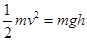 (2)
(2)h为木块所摆动的高度。解①,②联立方程组得到
v=8(m/s)
h=3.2(m)
【错解原因】这个解法是错误的。h=3.2m,就是木块摆动到了B点。如图所示。则它在B点时的速度vB。应满足方程
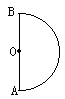
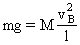
这时木块的重力提供了木块在B点做圆周运动所需要的向心力。解上述方程得
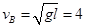 (m/s)
(m/s)如果vB<4 m/s,则木块不能升到B点,在到达B点之前的某一位置以某一速度开始做斜向上抛运动。而木块在B点时的速度vB=4m/s,是不符合机械能守恒定律的,木块在 B点时的能量为(选A点为零势能点)
木块在A点时的能量为
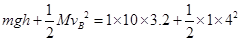
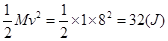
两者不相等。可见木块升不到B点,一定是h<3.2 m。
实际上,在木块向上运动的过程中,速度逐渐减小。当木块运动到某一临界位置C时,如图所示,木块所受的重力在绳子方向的分力恰好等于木块做圆周运动所需要的向心力。此时绳子的拉力为零,绳子便开始松弛了。木块就从这个位置开始,以此刻所具有的速度vc作斜上抛运动。木块所能到达的高度就是C点的高度和从C点开始的斜上抛运动的最大高度之和。
【正解】如上分析,从式①求得vA=v=8m/s。木块在临界位置C时的速度为vc,高度为
h′=l(1+cosθ) 如图所示,
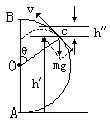
根据机船能守恒定律有
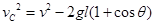 ③
③又
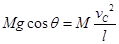 ,即
,即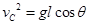 ④
④从式③和式④得
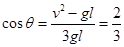
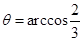
所以
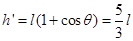
木块从C点开始以速度vc做斜上抛运动所能达到的最大高度h″为
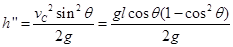
所以木块能达到的最大高度h为
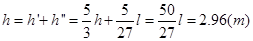
【点评】物体能否做圆运动,不是我们想象它怎样就怎样这里有一个需要的向心力和提供向心力能否吻合的问题,当需要能从实际提供中找到时,就可以做圆运动。所谓需要就是符合牛顿第二定律F向=ma向的力,而提供则是实际中的力若两者不相等,则物体将做向心运动或者离心运动。

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目



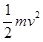
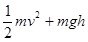
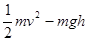
 37o。曲面所在区域和B点左下方的区域内都存在电场强度大小都为E的匀强电场,方向分别是水平向右和竖直向上。开始时有一质量为m的带电小球处于A点恰好保持静止。此后将曲面内的电场撤去,小球沿曲面下滑至B点时以速度V0水平抛出,最后落在电场内地面的P点,P点与B点间的水平距离为L。已知
37o。曲面所在区域和B点左下方的区域内都存在电场强度大小都为E的匀强电场,方向分别是水平向右和竖直向上。开始时有一质量为m的带电小球处于A点恰好保持静止。此后将曲面内的电场撤去,小球沿曲面下滑至B点时以速度V0水平抛出,最后落在电场内地面的P点,P点与B点间的水平距离为L。已知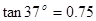 ,重力加速度为g。
,重力加速度为g。
 的圆弧轨道,O为圆心,OA水平,OB竖直,一小球从A点沿轨道射入,速度是v1,小球到达最高点B的速度是v2,则v1与v2比值可能是( )
的圆弧轨道,O为圆心,OA水平,OB竖直,一小球从A点沿轨道射入,速度是v1,小球到达最高点B的速度是v2,则v1与v2比值可能是( )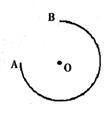
 : 1
: 1 从A点出发,沿两个不同的轨道滑行分别到达C点或D点后水平抛出。已知两个轨道是固定的而且光滑,A、B、E在同一水平地面上, C、D、E在同一竖直线上,D点距地面的高度为h,C点高度为2h, 重力加速度为g。
从A点出发,沿两个不同的轨道滑行分别到达C点或D点后水平抛出。已知两个轨道是固定的而且光滑,A、B、E在同一水平地面上, C、D、E在同一竖直线上,D点距地面的高度为h,C点高度为2h, 重力加速度为g。