题目内容
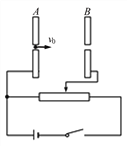
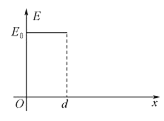
【题目】（20分）匀强电场的方向沿x轴正向，电场强度E随x的分布如图所示。图中E0和d均为已知量。将带正电的质点A在O点由能止释放。A离开电场足够远后，再将另一带正电的质点B放在O点也由静止释放，当B在电场中运动时，A、B间的相互作用力及相互作用能均为零；B离开电场后，A、B间的相作用视为静电作用。已知A的电荷量为Q，A和B的质量分别为m和
。不计重力。
（1）求A在电场中的运动时间t，
（2）若B的电荷量q =Q，求两质点相互作用能的最大值Epm
（3）为使B离开电场后不改变运动方向，求B所带电荷量的最大值qm
【答案】（1）
（2）QE0d （3）
Q
【解析】
解：（1）由牛顿第二定律得，A在电场中的加速度 a =
=
A在电场中做匀变速直线运动，由d =a
得
运动时间 t =
=
（2）设A、B离开电场时的速度分别为vA0、vB0，由动能定理得
QE0d =m
qE0d =
A、B相互作用过程中，动量和能量守恒。A、B相互作用为斥力，A受力与其运动方向相同，B受的力与其运动方向相反，相互作用力对A做正功，对B做负功。A、B靠近的过程中，B的路程大于A的路程，由于作用力大小相等，作用力对B做功的绝对值大于对A做功的绝对值，因此相互作用力做功之和为负，相互作用能增加。所以，当A、B最接近时相互作用能最大，此时两者速度相同，设为v，，
由动量守恒定律得：（m +
）v， = mvA0 +vB0
由能量守恒定律得：EPm= (m+)—
）
且 q =Q
解得相互作用能的最大值 EPm=QE0d
（3）A、B在x>d区间的运动，在初始状态和末态均无相互作用
根据动量守恒定律得：mvA+vB= mvA0 +vB0
根据能量守恒定律得：m
+
=m+
解得：vB = -
+
因为B不改变运动方向，所以vB = -+≥0
解得： q≤Q
则B所带电荷量的最大值为：qm =Q
出彩同步大试卷系列答案
【题目】小明同学在做“研究匀变速直线运动”实验中，选取其中一条纸带，在打点计时器打出的纸带上确定出7个计数点，相邻两个计数点之间的时间间隔为0.1s，并用刻度尺测出了各计数点到0计数点的距离，图中所标数据的单位是cm．
根据纸带提供的信息，小华同学已经计算出了打下1、2、4、5这五个计数点时小车的速度，请你帮助他计算出打下计数点3时小车的速度v3=__________m/s（结果保留3位有效数字），并填入下表．
| 1 | 2 | 3 | 4 | 5 |
t/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
v/（m．s） | 0.358 | 0.400 | 0.485 | 0.530 |
（2）以速度v为纵轴、时间t为横轴在坐标纸上建立直角坐标系，根据上表中的v、t数据，在坐标系中描点，并作出小车运动的v-t图像_____（图像作在答题纸上）．
（3）根据v﹣t图像可知，小车在0点的速度v0=__________m/s（保留3位有效数字）；小车运动的加速度为__________m/s2（保留2位有效数字）．
