题目内容
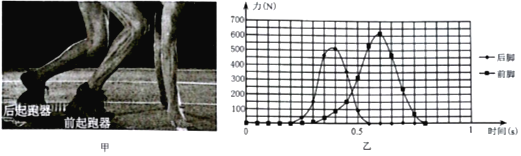
【题目】如图甲所示,一名百米短跑运动员正以蹲踞式起跑,他的双脚分别置于前、后起跑器上,发令枪响后,运动员对前、后起跑器作用力的水平分量随时间的变化关系如图乙所示,若运动员的质量为60kg,则在这次起跑过程中( )
A. 运动员的反应时间约0.2s
B. 运动员水平方向的最大加速度约10m/s2
C. 运动员刚离开起跑器时的水平速度大小约3.4m/s
D. 起跑器对运动员做功约350J
【答案】ABC
【解析】
A、由图可知,运动员在0.2s产生了力的作用,故说明此时产生反应,故反应时间为0.2s,故A正确。
B、由图可知,运动员水平方向受到的最大力约为600N,则由牛顿第二定律可知,最大加速度约为10m/s2;故B正确。
C、F-t图象中图象与时间轴所围成的面积可表示力的冲量,由图可知,冲量大小约为2040Nm,则由动量定理可知,I=mv,解得v约为3.4m/s,故C正确。
D、由于起跑器对人的力没有产生位移,故起跑器对人不做功,人的动能主要来自于人体内部做功消耗的生物能,故D错误。
故选ABC。

 阅读快车系列答案
阅读快车系列答案【题目】(1)某同学在用油膜法估测分子直径实验中,计算结果明显偏大,可能是由于 :
A.油酸未完全散开 |
B.油酸中含有大量的酒精 |
C.计算油膜面积时舍去了所有不足一格的方格 |
D.求每滴体积时,lmL的溶液的滴数误多记了10滴 |
(2)在做“用油膜法估测分子大小”的实验时,油酸酒精溶液的浓度为每1000mL溶液中有纯油酸1mL,用注射器测得1mL上述溶液有200滴,把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里,待水面稳定后,测得油酸膜的近似轮廓如图所示,图中正方形小方格的边长为1cm,则每一滴油酸酒精溶液中含有纯油酸的体积是 mL,油酸膜的面积是 cm2.根据上述数据,估测出油酸分子的直径是 m.