题目内容
1.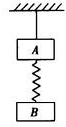 如图所示,质量相等的两个物体A、B之间用一轻弹簧相连,再用一细线悬挂在天花板上静止,当剪断细线的瞬间两物体的加速度各为多少( )
如图所示,质量相等的两个物体A、B之间用一轻弹簧相连,再用一细线悬挂在天花板上静止,当剪断细线的瞬间两物体的加速度各为多少( )| A. | A是0,B是g | B. | A是g、B是g | C. | A是2g、B是0 | D. | A是$\frac{g}{2}$、B是0 |
分析 剪断细线的瞬间,弹簧的弹力不变,分析两个物体的受力情况,根据牛顿第二定律求出物体A、B的瞬时加速度.
解答 解:设A、B的质量均为m.剪断细线前,对整体分析,绳的拉力为 T=2mg,弹簧的弹力为 F=mg.
剪断细线的瞬间,弹簧的弹力不变,对A,受重力和弹簧的弹力,瞬间的加速度 aA=$\frac{mg+F}{m}$=2g,方向竖直向下.对B,受重力和弹簧的弹力,受力情况不变,故B的加速度仍为0,故C正确,ABD错误.
故选:C
点评 本题是牛顿第二定律的瞬时问题,关键要明确弹簧的弹力不能发生突变,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
16.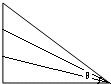 如图所示,一物体从底边相等(均为l)的各种长度不等的光滑斜面顶端由静止滑下,则当斜面倾角θ=45°时,物体滑到斜面底部所用时间最短,最短时间tmin=2$\sqrt{\frac{l}{g}}$.
如图所示,一物体从底边相等(均为l)的各种长度不等的光滑斜面顶端由静止滑下,则当斜面倾角θ=45°时,物体滑到斜面底部所用时间最短,最短时间tmin=2$\sqrt{\frac{l}{g}}$.
 如图所示,一物体从底边相等(均为l)的各种长度不等的光滑斜面顶端由静止滑下,则当斜面倾角θ=45°时,物体滑到斜面底部所用时间最短,最短时间tmin=2$\sqrt{\frac{l}{g}}$.
如图所示,一物体从底边相等(均为l)的各种长度不等的光滑斜面顶端由静止滑下,则当斜面倾角θ=45°时,物体滑到斜面底部所用时间最短,最短时间tmin=2$\sqrt{\frac{l}{g}}$.
10.宇宙飞船绕地球飞行时,从离地面较远的圆形轨道变轨到离地面较近的圆形轨道后( )
| A. | 周期减小 | B. | 周期不变 | C. | 线速度增大 | D. | 线速度不变 |
11.一质量为m的质点以速度v0匀速直线运动,在t=0时开始受到恒力F作用,速度大小先减小后增大,其最小值为v=0.5v0,由此可判断( )
| A. | 质点受力F作用后一定做匀变速曲线运动 | |
| B. | 质点受力F作用后可能做圆周运动 | |
| C. | t=0时恒力F与速度v0方向间的夹角为60° | |
| D. | t=$\frac{\sqrt{3}m{v}_{0}}{2F}$时,质点速度最小 |

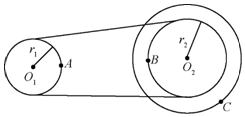 如图所示,O1皮带传动装置的主动轮的轴心,轮的半径为r1,O2为从动轮的轴心,轮的半径为r2,r3为与从动轮固定在一起的大轮的半径.已知r2=2r1,r3=3r1,A、B、C分别是三个轮边缘上的点,那么质点A、B、C的角速度之比是2:1:1向心加速度之比是4:2:3.
如图所示,O1皮带传动装置的主动轮的轴心,轮的半径为r1,O2为从动轮的轴心,轮的半径为r2,r3为与从动轮固定在一起的大轮的半径.已知r2=2r1,r3=3r1,A、B、C分别是三个轮边缘上的点,那么质点A、B、C的角速度之比是2:1:1向心加速度之比是4:2:3. 一辆平板式大货车载着一个木箱在平直公路上匀速行驶,已知木箱前部与驾驶室后部的距离为L=6m,如图所示.木箱与车厢底板的动摩擦因数为μ=0.4车厢的底板保持水平,且认为木箱与车厢底板的最大静摩擦力等于滑动摩擦力,g=10m/s2.
一辆平板式大货车载着一个木箱在平直公路上匀速行驶,已知木箱前部与驾驶室后部的距离为L=6m,如图所示.木箱与车厢底板的动摩擦因数为μ=0.4车厢的底板保持水平,且认为木箱与车厢底板的最大静摩擦力等于滑动摩擦力,g=10m/s2.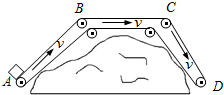 为了将物体从小山坡的A端运送到D端,设计了如图所示的传送皮带,其左边倾斜部分AB的长度为20m,AB与水平面的夹角为α=37°,水平部分BC的长度为16.25m,右边倾斜部分CD的长度为16.875m,CD与水平面的夹角为θ=53°.将一物体(可视为质点)轻轻放于A端的传送带上,物体与传送带间的动摩擦因数为μ=0.8.传送带沿图示方向以v=6m/s的速度匀速运动,若物体始终未脱离皮带,试求物体从A端被传送到D端所用的时间.(g=10m/s2,sin37°=0.6,cos37°=0.8,sin53°=0.8,cos53°=0.6)
为了将物体从小山坡的A端运送到D端,设计了如图所示的传送皮带,其左边倾斜部分AB的长度为20m,AB与水平面的夹角为α=37°,水平部分BC的长度为16.25m,右边倾斜部分CD的长度为16.875m,CD与水平面的夹角为θ=53°.将一物体(可视为质点)轻轻放于A端的传送带上,物体与传送带间的动摩擦因数为μ=0.8.传送带沿图示方向以v=6m/s的速度匀速运动,若物体始终未脱离皮带,试求物体从A端被传送到D端所用的时间.(g=10m/s2,sin37°=0.6,cos37°=0.8,sin53°=0.8,cos53°=0.6) 如图所示,水平地面上,光滑物块甲从A点在外力作用下以a1=4m/s2的加速度由静止开始向右运动,同时物块乙从B点以初速度v0水平向左运动.从甲、乙开始运动计时,经时间t=1.0s两物块相遇.已知物块乙与水平面间的动摩擦因数μ=0.2,A、B两点间的距离s=4m.取重力加速度g=10m/s2,求:
如图所示,水平地面上,光滑物块甲从A点在外力作用下以a1=4m/s2的加速度由静止开始向右运动,同时物块乙从B点以初速度v0水平向左运动.从甲、乙开始运动计时,经时间t=1.0s两物块相遇.已知物块乙与水平面间的动摩擦因数μ=0.2,A、B两点间的距离s=4m.取重力加速度g=10m/s2,求: