题目内容
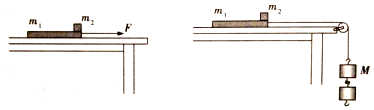
9．
一辆平板式大货车载着一个木箱在平直公路上匀速行驶，已知木箱前部与驾驶室后部的距离为L=6m，如图所示．木箱与车厢底板的动摩擦因数为μ=0.4车厢的底板保持水平，且认为木箱与车厢底板的最大静摩擦力等于滑动摩擦力，g=10m/s2．（1）为了使木箱在车厢底板上不发生相对滑动，求货车刹车的加速度a的范围
（2）若货车某次刹车的加速度恒为6m/s2，为了保证木箱在此次刹车期间不撞上驾驶室，此次刹车最多持续多长时间？（设刹车后货车匀速运动．）
分析 （1）隔离对木箱分析，根据最大静摩擦力求出临界的加速度，求得刹车时的最大加速度，从而得到货车刹车的加速度a的范围．
（2）若货车某次刹车的加速度恒为6m/s2，求出木箱与车间的相对加速度，通过相对位移，结合运动学公式，求出刹车最多持续的时间．
解答 解：（1）木箱与车厢底板的最大静摩擦力为 fm=μmg．
为了使木箱在车厢底板上不发生相对滑动，木箱的最大加速度 a=$\frac{{f}_{m}}{m}$=μg=4m/s2．
所以货车刹车的最大加速度a为4m/s2，货车刹车的加速度a的范围为0＜a＜4m/s2．
（2）当货车刹车，木箱相对车厢发生相对移动，木箱相对于车厢的加速度大小 a1=a'-a=6m/s2-4m/s2=2m/s2
初速度为零，则有 L=$\frac{1}{2}$a1t2
解得 t=$\sqrt{\frac{2L}{{a}_{1}}}$=$\sqrt{\frac{2×6}{2}}$=$\sqrt{6}$s．
答：
（1）货车刹车的加速度a的范围为0＜a＜4m/s2．
（2）此次刹车最多持续时间是$\sqrt{6}$s．
点评 本题要知道加速度是联系力学和运动学的桥梁，当两个发生相对滑动时，可用相对加速度和位移求时间，也可以通过货车和木箱的位移关系，结合运动学公式进行求时间．
练习册系列答案
名校课堂系列答案
相关题目
18．氢原子的核外电子由离原子核较远的轨道跃迁到离核较近的轨道上时，下列说法中正确的是（ ）
| A． | 核外电子的动能增大 | B． | 氢原子的能量增大 | ||
| C． | 氢原子要吸收一定频率的光子 | D． | 核外电子的转动周期变大 |
19．关于电场场强的概念，下列说法正确的是（ ）
| A． | 由 E=$\frac{F}{q}$可知，某电场的场强 E 与 q 成反比，与 F 成正比 | |
| B． | 正负试探电荷在同一点受到的电场力方向相反，所以某一点场强方向与试探电荷的正负有关 | |
| C． | 电场中某一点的场强与放入该点的试探电荷正负无关 | |
| D． | 电场中某一点不放试探电荷时，该点场强等于零 |
16．
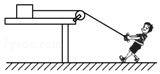如图所示，光滑水平平台上有一个质量为m的物块，站在地面上的人用跨过定滑轮的绳子向右拉动物块，不计绳和滑轮的质量及滑轮的摩擦，且平台边缘离人手作用点竖直高度始终为h．当人以速度v从平台的边缘处向右匀速前进位移x时，则（ ）
如图所示，光滑水平平台上有一个质量为m的物块，站在地面上的人用跨过定滑轮的绳子向右拉动物块，不计绳和滑轮的质量及滑轮的摩擦，且平台边缘离人手作用点竖直高度始终为h．当人以速度v从平台的边缘处向右匀速前进位移x时，则（ ）| A． | 在该过程中，物块做加速运动 | |
| B． | 在该过程中，人对物块做的功为$\frac{m{v}^{2}{x}^{2}}{2（{h}^{2}+{x}^{2}）}$ | |
| C． | 在该过程中，人对物块做的功为$\frac{1}{2}$mv2 | |
| D． | 人前进x时，物块的运动速率为$\frac{vx}{\sqrt{{x}^{2}+{h}^{2}}}$ |
4．
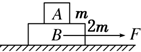如图所示，水平面上放置质量分别为m、2m的A、B两个物体，A、B间，B与地面间动摩擦因数均为μ，最大静摩擦力等于滑动摩擦力，现用水平拉力F拉B，使A、B一起以同一加速度运动，则拉力F的最大值为（ ）
如图所示，水平面上放置质量分别为m、2m的A、B两个物体，A、B间，B与地面间动摩擦因数均为μ，最大静摩擦力等于滑动摩擦力，现用水平拉力F拉B，使A、B一起以同一加速度运动，则拉力F的最大值为（ ）| A． | 6μmg | B． | 3μmg | C． | μmg | D． | 4μmg |
14．
如图所示，质量均为m的A、B两球之间系着一条轻弹簧放在光滑的水平面上，A球靠紧墙壁，现用力F将B球向左推压弹簧，平衡后，突然将力F撤去的瞬间，则（ ）
如图所示，质量均为m的A、B两球之间系着一条轻弹簧放在光滑的水平面上，A球靠紧墙壁，现用力F将B球向左推压弹簧，平衡后，突然将力F撤去的瞬间，则（ ）| A． | 突然将F撤去瞬间，两球的速度和加速度均为0 | |
| B． | A球离开墙壁后，两球的速度相等时弹簧恰好恢复原长 | |
| C． | B球运动过程中加速度的最大值为$\frac{F}{2m}$ | |
| D． | A球离开墙壁后，两球的加速度始终大小相等，方向相反 |
1．
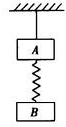如图所示，质量相等的两个物体A、B之间用一轻弹簧相连，再用一细线悬挂在天花板上静止，当剪断细线的瞬间两物体的加速度各为多少（ ）
如图所示，质量相等的两个物体A、B之间用一轻弹簧相连，再用一细线悬挂在天花板上静止，当剪断细线的瞬间两物体的加速度各为多少（ ）| A． | A是0，B是g | B． | A是g、B是g | C． | A是2g、B是0 | D． | A是$\frac{g}{2}$、B是0 |
19．已知地球半径为R．同步卫星的轨道半径为r．赤道上的物体和近地卫星加速度分别为a1、a2，速度分别为v1、v2，则以下关系正确的是（ ）
| A． | $\frac{{a}_{1}}{{a}_{2}}=\frac{{R}^{3}}{{r}^{3}}$ | B． | $\frac{{v}_{1}}{{v}_{2}}=\frac{R}{r}\sqrt{\frac{R}{r}}$ | C． | $\frac{{a}_{1}}{{a}_{2}}=\frac{R}{r}\sqrt{\frac{R}{r}}$ | D． | $\frac{{v}_{1}}{{v}_{2}}=\frac{{R}^{3}}{{r}^{3}}$ |