题目内容
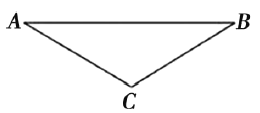
【题目】在竖直墙壁的左侧水平地面上,放置一个边长为a、质量为M的正方体ABCD,在墙壁和正方体之间放置一半径为R、质量为m的光滑球,正方体和球均保持静止,如图所示。球的球心为O,OB与竖直方向的夹角为![]() ,正方体的边长a>R,正方体与水平地面的动摩擦因数为
,正方体的边长a>R,正方体与水平地面的动摩擦因数为![]() 。(g已知,并取最大静摩擦力等于滑动摩擦力)求:
。(g已知,并取最大静摩擦力等于滑动摩擦力)求:
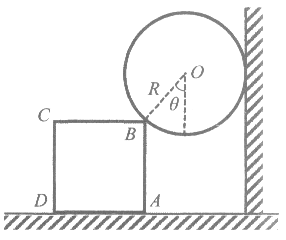
(1)正方体和墙壁对球的支持力N1、N2分别是多大?
(2)若![]() =45°,保持球的半径不变,只增大球的质量,为了不让正方体出现滑动,则球质量的最大值为多少?(tan45°=1)。
=45°,保持球的半径不变,只增大球的质量,为了不让正方体出现滑动,则球质量的最大值为多少?(tan45°=1)。
(3)改变正方体到墙壁之间的距离,球和正方体都处于静止状态,且球没有掉落地面。若不让正方体出现滑动,讨论以下情况:
a. 若球的质量m=![]() M,则正方体的右侧面AB到墙壁的最大距离是多少?
M,则正方体的右侧面AB到墙壁的最大距离是多少?
b. 当正方体的右侧面AB到墙壁的距离小于某个值时,则无论球的质量是多少,正方体都不会滑动,则这个距离的值是多少?
【答案】(1)N1=mg/cos![]() ,N2=mgtan
,N2=mgtan![]() ;(2)m<
;(2)m<![]() ;(3)a.
;(3)a. ![]() R;b.
R;b. ![]() R。
R。
【解析】
(1)以球为研究对象,受力如图:
小球受力平衡:N1cosθ=mg,N1=![]()
N2=mgtanθ;
(2)以正方体和球整体为研究对象,竖直方向受重力(m+M)g和地面的支持力FN,水平方向受墙壁的弹力N2和地面的摩擦力Ff,则:
FN=(m+M)g
N2= mgtan45°<Ff
Ff=μFN
联立解得:m<![]() ;
;
(3)a、若球的质量m=![]() M,对整体
M,对整体
FN=(m+M)g
N2= mgtanθ<Ff
Ff=μFN
联立解得:θ<60°
正方体的右侧面AB到墙壁的最大距离:L=R+Rsin60°=![]() R;
R;
b、根据FN=(m+M)g
N2= mgtanθ<Ff
Ff=μFN
得:mgtanθ![]() μ(m+M)g
μ(m+M)g
tanθ![]()
![]()
tanθ![]()
![]() ,θ
,θ![]() 30°
30°
故L![]() R+Rsin30°=
R+Rsin30°=![]() R
R