题目内容
【题目】![]() 年
年![]() 月,天文学家们通过观测的数据确认了银河系中央的黑洞“人马座
月,天文学家们通过观测的数据确认了银河系中央的黑洞“人马座![]() ”的质量与太阳质量的倍数关系.研究发现,有一星体
”的质量与太阳质量的倍数关系.研究发现,有一星体![]() 绕人马座
绕人马座![]() 做椭圆运动,其轨道半长轴为
做椭圆运动,其轨道半长轴为![]() 天文单位(地球公转轨道的半径为一个天文单位),人马座
天文单位(地球公转轨道的半径为一个天文单位),人马座![]() 就处在该椭圆的一个焦点上.观测得到
就处在该椭圆的一个焦点上.观测得到![]() 星的运行周期为
星的运行周期为![]() 年.
年.
(![]() )若将
)若将![]() 星的运行轨道视为半径
星的运行轨道视为半径![]() 天文单位的圆轨道,试估算人马座
天文单位的圆轨道,试估算人马座![]() 的质量
的质量![]() 是太阳质量
是太阳质量![]() 的多少倍(结果保留一位有效数字);
的多少倍(结果保留一位有效数字);
(![]() )黑洞的第二宇宙速度极大,处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚.由于引力的作用,黑洞表面处质量为
)黑洞的第二宇宙速度极大,处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚.由于引力的作用,黑洞表面处质量为![]() 的粒子具有的势能为
的粒子具有的势能为![]() (设粒子在离黑洞无限远处的势能为零),式中
(设粒子在离黑洞无限远处的势能为零),式中![]() 、
、![]() 分别表示黑洞的质量和半径.已知引力常量
分别表示黑洞的质量和半径.已知引力常量![]() ,光速
,光速![]() ,太阳质量
,太阳质量![]() ,太阳半径
,太阳半径![]() ,不考虑相对论效应,利用上问结果,在经典力学范围内求人马座
,不考虑相对论效应,利用上问结果,在经典力学范围内求人马座![]() 的半径
的半径![]() 与太阳半径
与太阳半径![]() 之比应小于多少(结果按四舍五入保留整数).
之比应小于多少(结果按四舍五入保留整数).
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:研究星![]() 绕人马座A*做圆周运动,根据万有引力提供向心力,列出等式求出人马座A*的质量.研究地球绕太阳做圆周运动,根据万有引力提供向心力,列出等式求出太阳的质量.根据题目提供的信息,筛选出有用的信息,结合功能关系,求出问题.
绕人马座A*做圆周运动,根据万有引力提供向心力,列出等式求出人马座A*的质量.研究地球绕太阳做圆周运动,根据万有引力提供向心力,列出等式求出太阳的质量.根据题目提供的信息,筛选出有用的信息,结合功能关系,求出问题.
(1)设![]() 星的质量为
星的质量为![]() ,角速度为
,角速度为![]() ,周期为
,周期为![]() ,根据万有引力提供向心力得:
,根据万有引力提供向心力得:
![]() ,又
,又![]()
设地球质量为![]() ,公转轨道半径为
,公转轨道半径为![]() ,周期为
,周期为![]() ,根据万有引力提供向心力得:
,根据万有引力提供向心力得:
![]() ,又
,又![]()
联立得: 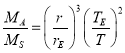 ,其中
,其中![]() 年,
年, ![]() 天文单位
天文单位
代入数据可得![]()
(2)引力对粒子作用不到的地方即为无限远,此时粒子的势能为零.粒子在到达无限远之前,其动能便减小为零,此时势能仍为负值,则其能量总和小于零,则有: ![]()
由题意可知![]() ,
, ![]()
可得: ![]()
代入数据得: ![]()
所以: ![]()

练习册系列答案
相关题目





