题目内容
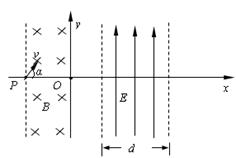
如图所示,直角坐标系xoy位于竖直平面内,在? m≤x≤0的区域内有磁感应强度大小B = 4.0×10-4T、方向垂直于纸面向里的条形匀强磁场,其左边界与x轴交于P点;在x>0的区域内有电场强度大小E = 4N/C、方向沿y轴正方向的条形匀强电场,其宽度d = 2m。一质量m = 6.4×10-27kg、电荷量q =3.2×10?19C的带负电粒子从P点以速度v = 4×104m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力。求:
m≤x≤0的区域内有磁感应强度大小B = 4.0×10-4T、方向垂直于纸面向里的条形匀强磁场,其左边界与x轴交于P点;在x>0的区域内有电场强度大小E = 4N/C、方向沿y轴正方向的条形匀强电场,其宽度d = 2m。一质量m = 6.4×10-27kg、电荷量q =3.2×10?19C的带负电粒子从P点以速度v = 4×104m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力。求:
⑴带电粒子在磁场中运动时间;
⑵当电场左边界与y轴重合时Q点的横坐标;
⑶若只改变上述电场强度的大小,要求带电粒子仍能通过Q点,讨论此电场左边界的横坐标x′与电场强度的大小E′的函数关系。
 m≤x≤0的区域内有磁感应强度大小B = 4.0×10-4T、方向垂直于纸面向里的条形匀强磁场,其左边界与x轴交于P点;在x>0的区域内有电场强度大小E = 4N/C、方向沿y轴正方向的条形匀强电场,其宽度d = 2m。一质量m = 6.4×10-27kg、电荷量q =3.2×10?19C的带负电粒子从P点以速度v = 4×104m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力。求:
m≤x≤0的区域内有磁感应强度大小B = 4.0×10-4T、方向垂直于纸面向里的条形匀强磁场,其左边界与x轴交于P点;在x>0的区域内有电场强度大小E = 4N/C、方向沿y轴正方向的条形匀强电场,其宽度d = 2m。一质量m = 6.4×10-27kg、电荷量q =3.2×10?19C的带负电粒子从P点以速度v = 4×104m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力。求:
⑴带电粒子在磁场中运动时间;
⑵当电场左边界与y轴重合时Q点的横坐标;
⑶若只改变上述电场强度的大小,要求带电粒子仍能通过Q点,讨论此电场左边界的横坐标x′与电场强度的大小E′的函数关系。
⑴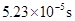 ⑵x=5m ⑶
⑵x=5m ⑶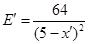
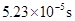 ⑵x=5m ⑶
⑵x=5m ⑶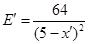
试题分析:⑴带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律有

代入数据得:
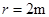
轨迹如图1交y轴于C点,过P点作v的垂线交y轴于O1点,
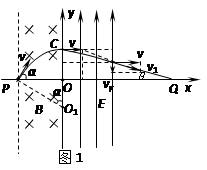
由几何关系得
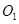 为粒子运动轨迹的圆心,且圆心角为60°。
为粒子运动轨迹的圆心,且圆心角为60°。 在磁场中运动时间
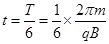
代入数据得:
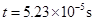
⑵带电粒子离开磁场垂直进入电场后做类平抛运动
方法一:
粒子在电场中加速度
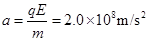
运动时间
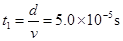
沿y方向分速度
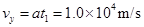
沿y方向位移
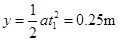
粒子出电场后又经时间t2达x轴上Q点
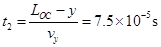
故Q点的坐标为
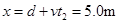
方法二:
设带电粒子离开电场时的速度偏向角为θ,如图1,则:
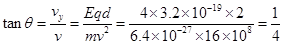
设Q点的横坐标为x
则:
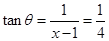
故x=5m。
⑶电场左边界的横坐标为x′。
当0<x′<3m时,如图2,

设粒子离开电场
时的速度偏向角为θ′,
则:

又:
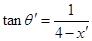
由上两式得:
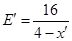
当3m≤
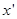 ≤5m时,如图3,
≤5m时,如图3,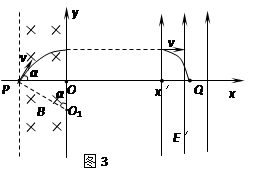
有
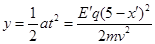
将y=1m及各数据代入上式得:
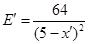
点评:此题要求首先要分析粒子在各个区域内的运动情况,必要时画出粒子的运动轨迹图,了解图中的几何关系.利用粒子在电场中偏转时的速度的合成与分解,解决电子在电场中运动的相关问题;利用粒子在匀速圆周运动的半径和周期公式,结合洛伦兹力提供向心力可解答粒子在磁场中运动的相关问题。

练习册系列答案
相关题目


 时间内,电场力对粒子做功为
时间内,电场力对粒子做功为

 和后
和后
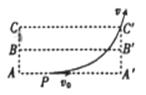
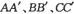 是该电场的三个等势面,相邻等势面间的距离为1 cm,其中
是该电场的三个等势面,相邻等势面间的距离为1 cm,其中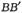 为零电势能面.一质量为m、带电織为+q的粒子沿AA'方向以初速度v0自图中的P点进入电场,刚好从C’点离开电场.已知
为零电势能面.一质量为m、带电織为+q的粒子沿AA'方向以初速度v0自图中的P点进入电场,刚好从C’点离开电场.已知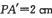 粒子的重力忽略不计.倾说法中正确的是( )
粒子的重力忽略不计.倾说法中正确的是( )