题目内容
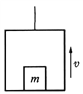
【题目】如图所示,在水平面上固定放置一个倾角为37°的光滑斜面,一物块以v0=6m/s的初速度从斜面底端滑上斜面,恰好能到达斜面顶端。
(1)斜面的长度;
(2)在斜面上设置一个长度为d=0.75m的摩擦区,物块与摩擦区之间的动摩擦因数μ=0.25,要使木块在上滑过程中不滑出摩擦区,求摩擦区下边界到斜面底端的最小距离;
(3)由于摩擦区的存在,使物体上滑时间(从开始运动到速度减为零的时间)减少了t,请写出t与摩擦区下边界到斜面底端距离x的关系式。

【答案】(1)3m; (2)2m; (3)![]() ,
,![]() ;
;
![]() ,
,![]()
【解析】
(1)g取10m/s2,对物块,由牛顿第二定律
![]()
得加速度
![]()
位移为
![]()
即为斜面长度;
(2)当物块在上滑过程中恰好不滑出摩擦区时,摩擦区下边界到斜面底端距离最小。设最小距离为![]() ,此时物块到达摩擦区上边界时速度恰好为0。
,此时物块到达摩擦区上边界时速度恰好为0。
![]()
在摩擦区,对物块,由牛顿第二定律得加速度
![]()
可得摩擦区下边界到斜面底端的最小距离为
![]() ;
;
(3)没有摩擦区,上滑时间
![]()
有摩擦区,设上滑时间为![]() 。
。
a.当![]()
![]()
![]()
得
![]()
![]()
得
![]()
![]()
![]()
![]()
b.当![]() ,
,
![]()
![]()
![]()
得
![]()
![]() 。
。

练习册系列答案
相关题目