题目内容
【题目】如图所示，轻杆长为3L，在杆的A、B两端分别固定质量均为m的球A和球B，杆上距球A为L处的点O装在光滑的水平转动轴上，杆和球在竖直面内转动，已知球B运动到最高点时，球B对杆恰好无作用力．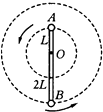
求：
（1）球B在最高点时，杆对A球的作用力大小．
（2）若球B转到最低点时B的速度vB= 
，杆对球A和球B的作用力分别是多大？A球对杆的作用力方向如何？
【答案】
（1）
解：球B在最高点时速度为v0，有 
，
得： 
．
因为A、B两球的角速度相等，根据v=rω知，此时球A的速度为： 
设此时杆对球A的作用力为FA，则 FA﹣mg=m 
解得：FA=1.5mg
（2）
解：若球B转到最低点时B的速度vB= 
，则对B球得：
解得：FB=3.6mg
此时A球的速度 vA= 
vB= 
，则 
则杆对A球作用力的方向向下，牛顿第三定律得，A球对杆作用力的方向向上．
由牛顿第二定律得： 
解得：FA=0.3mg
【解析】（1）抓住B球在最高点对杆子的作用力为零，结合牛顿第二定律求出B球的速度，根据A、B角速度相等，得出A、B的线速度关系，从而对A分析，根据牛顿第二定律求出杆子对A的作用力大小．（2）再根据牛顿第二定律求出杆对两球的作用力的大小和方向．并确定出A球对杆的作用力方向．
【考点精析】根据题目的已知条件，利用牛顿第三定律和向心力的相关知识可以得到问题的答案，需要掌握牛顿第三运动定律指出了两物体之间的作用是相互的，因而力总是成对出现的，它们总是同时产生，同时消失；作用力和反作用力总是同种性质的力；作用力和反作用力分别作用在两个不同的物体上，各产生其效果，不可叠加；向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力．
