Question

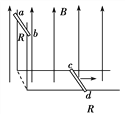
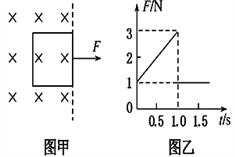
【题目】一正方形金属线框位于有界匀强磁场区域内，线框平面与磁场垂直，线框的右边紧贴着磁场边界，如图甲所示。t＝0时刻对线框施加一水平向右的外力，让线框从静止开始做匀加速直线运动穿过磁场，外力F随时间t变化的图象如图乙所示。已知线框质量m＝1 kg、电阻R＝ 1Ω，以下说法正确的是( )

A. 线框做匀加速直线运动的加速度为1 m/s2

B. 匀强磁场的磁感应强度为2T

C. 线框穿过磁场的过程中，通过线框的电荷量为C

D. 线框边长为1 m

Answer 1

【答案】ABC

【解析】t=0时刻，线框的速度为零，线框没有感应电流，不受安培力，加速度为： ，故A正确；线框刚出磁场时的速度为 v=at=1×1m/s=1m/s，此时线框所受的安培力为FA=BIL， ，则得 ，根据牛顿第二定律得 F-FA=ma，代入得 F-=ma，代入数据 F=3N，m=1kg，R=1Ω，L=0.5m，v=1m/s，a=1m/s2解得，B=2 T，故B正确；线框的边长为：L=at2=×1×12=0.5m，故D错误；电荷量： ，电流： ，由法拉第电磁感应定律得： ，则得通过线框的电量： ，故C正确．故选ABC．