题目内容
【题目】如图是一个半径为R、球心为O的半球形透明玻璃体的截面图。在距离O点右侧1.5R处有一个竖直放置的幕布MN，OA为球体的一条水平轴线且与幕布MN垂直.
(i)某光源发出的细光线沿OA方向从O点射入半球形透明玻璃体并在幕布上形成二亮斑。现保持光线的传播方向不变让光源缓慢下移，当射入点位于O点正下方
时，幕布上的亮斑突然消失，求该透明玻璃半球体折射率；
（ii）若将该光源置于O点左侧
处的S点，其发出的一细光线沿与OA夹角
方向射向该透明玻璃半球体，求光线由光源到达幕布所用时间. (已知光在真空中传播速度为c，不考虑光线在透明玻璃内的二次反射) .
【答案】(i)
（ii）
【解析】
(1)如图1所示:
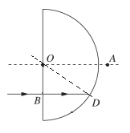
根据几何关系有：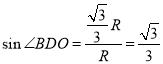
①
细光束在B点水平入射，在D点发生全反射，根据折射定律：
则 ②
(2)作光路图如图2所示:
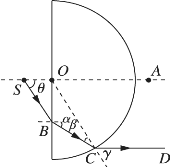
由几何关系可得:
由折射定律可得
③
解得:α＝30°
在△OBC中，
④
计算可得 β=30° ⑤
根据折射定律：
⑥
解得: γ＝60°
光线第一次从玻璃半球体水平出射，即出射光线CD方向与OA平行向右.
在玻璃半球体中传播的距离lBC＝lOB，C点到幕布的距离为l=1.5R-Rsin30°=R
由折射率与光速关系得：
⑦
解得:
⑧
练习册系列答案
相关题目
