题目内容
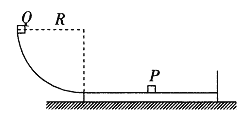
【题目】如图所示,竖直平面内固定有半径R=1.8m的![]() 光滑圆弧轨道,轨道末端水平且与放在水平地面上的长木板的上表面等高。长木板上表面光滑,下表面与水平地面间的动摩擦因数
光滑圆弧轨道,轨道末端水平且与放在水平地面上的长木板的上表面等高。长木板上表面光滑,下表面与水平地面间的动摩擦因数![]() = 0.1,木板正中间放有一质量m=lkg的滑块P,木板上表面右端固定有一带有橡皮泥的挡板。现将一质量也为1kg的滑块Q从圆弧轨道的最高点由静止释放,当其刚滑上长木板时给滑块P一个向左的初速度v=3m/s,P,Q发生弹性正碰后滑块P运动到木板右端与挡板粘在一起继续运动。已知长木板的质量 M= 5kg,长l= 9m,重力加速度g =10m/ s2 ,滑块P,Q均可视为质点。求:
= 0.1,木板正中间放有一质量m=lkg的滑块P,木板上表面右端固定有一带有橡皮泥的挡板。现将一质量也为1kg的滑块Q从圆弧轨道的最高点由静止释放,当其刚滑上长木板时给滑块P一个向左的初速度v=3m/s,P,Q发生弹性正碰后滑块P运动到木板右端与挡板粘在一起继续运动。已知长木板的质量 M= 5kg,长l= 9m,重力加速度g =10m/ s2 ,滑块P,Q均可视为质点。求:
(1)P,Q发生弹性正碰后各自的速度;
(2)长木板运动的位移大小。
【答案】(1) ![]() m/s,
m/s,![]() m/s (2) x=0.5m
m/s (2) x=0.5m
【解析】
(1)由机械能守恒定律可知:![]()
解得:![]() m/s
m/s
两滑块作用过程中,以向右的方向为正,由动量守恒定律、机械能守恒定律可知:
![]()
![]()
解得:![]() m/s,
m/s,![]() m/s
m/s
(2)两滑块相碰前的位移大小之和为![]() m,则有:
m,则有:![]()
则滑块P向左运动的位移大小为1.5m,滑块Q向右运动的位移大小为3m,两滑块相碰后,Q向左运动![]() s后离开木板,P向右运动
s后离开木板,P向右运动![]() s后与挡板相撞,相撞过程中动量守恒,则有:
s后与挡板相撞,相撞过程中动量守恒,则有:![]()
相撞后P与木板一起运动,则有:![]() ,其中
,其中![]()
解得:x=0.5m

【题目】某同学在测量电源的电动势和内阻的实验中,由于所用的电压表(可视为理想表)的量程不够大,设计了如图所示的电路。
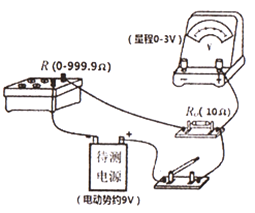
(1)该同学在连接电路时,还剩下连接电压表的一条导线没连好,请帮他补充完整________。在开关闭合前先将电阻箱的电阻调到处____________(选填“最大值”、“最小值”或“任意值”)。
(2)改变电阻箱的阻值R,分别测出当定值电阻阻值为![]() 时,电压表两端的电压为U,下列两组关于电阻箱的取值方案中,比较合理的方案是____________. (选填“甲”或“乙”)
时,电压表两端的电压为U,下列两组关于电阻箱的取值方案中,比较合理的方案是____________. (选填“甲”或“乙”)
方案编号 | 电阻箱的阻值 | ||||
甲 | 400. 0 | 350. 0 | 300. 0 | 250. 0 | 200. 0 |
乙 | 80. 0 | 70. 0 | 60. 0 | 50. 0 | 40. 0 |
(3)根据实验数据描点,绘出的![]() 图象是一条直线,若直线的斜率为k,在
图象是一条直线,若直线的斜率为k,在![]() 坐标轴上的截距为b,则该电源的电动势E =____________,内阻r=____________(用k、b和R0表示)
坐标轴上的截距为b,则该电源的电动势E =____________,内阻r=____________(用k、b和R0表示)