题目内容
13.车站、码头、机场等使用的货物安检装置的示意图如图所示,绷紧的传送带始终保持υ=1m/s的恒定速率运行,AB为水平传送带部分且足够长,现有一质量为m=5kg的行李包(可视为质点)无初速度的放在水平传送带的A端,传送到B端时没有被及时取下,行李包从B端沿倾角为37°的斜面滑入储物槽,已知行李包与传送带的动摩擦因数为0.5,行李包与斜面间的动摩擦因数为0.8,g=10m/s2,不计空气阻力(sin37°=0.6,cos37°=0.8).
(1)行李包相对于传送带滑动的距离.
(2)若B轮的半径为R=0.2m,求行李包在B点对传送带的压力;
(3)若行李包滑到储物槽时的速度刚好为零,求斜面的长度.
分析 (1)水平方向行李包受到摩擦力的作用做匀加速直线运动,由牛顿第二定律求出加速度,由v=at求出运动的时间,根据时间和加速度求出水平距离以及二者水平位移的差.
(2)行李包在B点受到重力和支持力的作用,由牛顿第二定律即可求得支持力;压力大小等于支持力;
(3)根据受力分析,结合牛顿第二定律求出行李包在斜面上的加速度,然后结合题目的条件即可求出.
解答 解:(1)行李包在水平传送带上有摩擦力产生加速度,由牛顿第二定律得:
μ1mg=ma1
所以:${a}_{1}={μ}_{1}g=0.5×10=5m/{s}^{2}$
行李包到达传送带的速度需要的时间:v=a1t1
所以:${t}_{1}=\frac{v}{{a}_{1}}=\frac{1}{5}=0.2$s
行李包前进的距离:${x}_{1}=\frac{1}{2}{a}_{1}{t}_{1}^{2}$
传送带前进的距离:x2=vt1
行李包相对于传送带的距离:△x=x2-x1
代入数据解得:△x=0.1 m
(2)行李包在B点受到重力和支持力的作用,由牛顿第二定律可知:
mg-F=$\frac{m{v}^{2}}{R}$
代入数据得:F=25N
根据牛顿第三定律,行李包在B点对传送带的压力大小是25N,方向竖直向下.
(3)行李包在斜面上受到重力、支持力和摩擦力的作用,沿斜面向下的方向:
μ2mgcos37°-mgsin37°=ma2
要使它到达底部时的速度恰好为0,则:0-v2=-2a2x
代入数据解得:x=1.25m
答:(1)行李包相对于传送带滑动的距离是0.1m.
(2)若B轮的半径为R=0.2m,行李包在B点对传送带的压力是25N,方向竖直向下;
(3)若行李包滑到储物槽时的速度刚好为零,斜面的长度是1.25m.
点评 该题考查牛顿运动定律的综合应用,属于单物体多过程的情况,这一类的问题要理清运动的过程以及各过程中的受力,然后再应用牛顿运动定律解答.

| A. | 抛射角一定时,初速度越大,飞行时间越长 | |
| B. | 初速度一定时,抛射角越大,射高越小 | |
| C. | 初速度一定时,抛射角越大,射程一定越大 | |
| D. | 到达最高点时,物体速度为零,加速度不为零 |
| A. | $\frac{mv}{M-m}$ | B. | -$\frac{mv}{M+m}$ | C. | $\frac{mv}{M+m}$ | D. | -$\frac{mv}{M-m}$ |
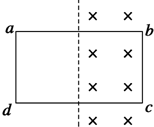 如图所示,开始时矩形线框与匀强磁场的方向垂直,且一半在磁场内,一半在磁场外.若要使线框中产生感应电流,下列办法中可行的是( )
如图所示,开始时矩形线框与匀强磁场的方向垂直,且一半在磁场内,一半在磁场外.若要使线框中产生感应电流,下列办法中可行的是( )| A. | 以cd边为轴转动(小于90°) | B. | 以ab边为轴转动(小于90°) | ||
| C. | 以ad边为轴转动(小于60°) | D. | 以bc边为轴转动(小于60°) |
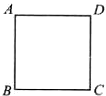 如图,一只蚂蚁从A点出发,沿边长为a的正方形路线爬行,经过B、C、D后又回到A点,则在这一过程中( )
如图,一只蚂蚁从A点出发,沿边长为a的正方形路线爬行,经过B、C、D后又回到A点,则在这一过程中( )| A. | 蚂蚁的位移大小为4a | B. | 蚂蚁的位移为零 | ||
| C. | 蚂蚁运动的路程为零 | D. | 蚂蚁运动的路程和位移都为零 |
| A. | 位移和时间均不同 | B. | 位移和时间均相同 | ||
| C. | 位移相同,时间不同 | D. | 位移不同,时间相同 |
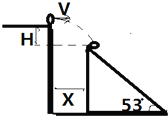 如图所示,一小球自平台上水平抛出,恰好落在平台前一倾角α=53°的斜面顶端,并刚好沿斜面下滑(此时速度方向沿斜面方向),已知斜面顶端与平台高度差h=0.8m,g=10m/s2,则小球水平抛出的初速度为3m/s,斜面与平台边缘的水平距离为1.2m.
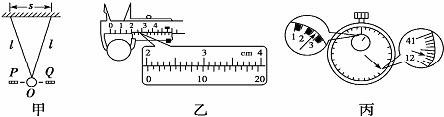
如图所示,一小球自平台上水平抛出,恰好落在平台前一倾角α=53°的斜面顶端,并刚好沿斜面下滑(此时速度方向沿斜面方向),已知斜面顶端与平台高度差h=0.8m,g=10m/s2,则小球水平抛出的初速度为3m/s,斜面与平台边缘的水平距离为1.2m.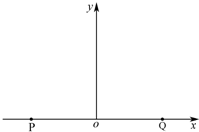 如图所示,在x轴上方有垂直于xOy平面向外的足够大匀强磁场(图中没有画出该磁场),一个质量为m,电荷量为q(q>0)的粒子,在P点以速率v沿与x轴成某一角度射入磁场,然后粒子从Q点离开磁场,P点与Q点关于y轴对称且相距为2a,其中a=$\frac{mv}{2Bq}$(B为磁感应强度,大小未知,不计粒子重力的影响).
如图所示,在x轴上方有垂直于xOy平面向外的足够大匀强磁场(图中没有画出该磁场),一个质量为m,电荷量为q(q>0)的粒子,在P点以速率v沿与x轴成某一角度射入磁场,然后粒子从Q点离开磁场,P点与Q点关于y轴对称且相距为2a,其中a=$\frac{mv}{2Bq}$(B为磁感应强度,大小未知,不计粒子重力的影响).