题目内容
(12分)如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10 27kg,电荷量q = 3.2×10 19C,初速度v = 3.2×106m/s。(sin37°= 0.6,cos37°= 0.8)求:

(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子穿出金箔进入电场,在电场中运动通过N点,SN⊥ab且SN = 40cm,则此α粒子从金箔上穿出时,损失的动能△EK为多少?
(1)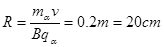 (2)
(2)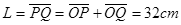
(3)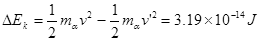
【解析】
试题分析:(1)α粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,即 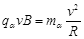 (1分)
(1分)
则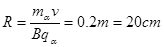 (2分)
(2分)
(2)设cd中心为O,向c端偏转的α粒子,当圆周轨迹与cd相切时偏离O最远,设切点为P,对应圆心O1,如图所示,则由几何关系得:
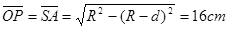 (1分)
(1分)
向d端偏转的α粒子,当沿sb方向射入时,偏离O最远,设此时圆周轨迹与cd交于Q点,对应圆心O2,如图所示,则由几何关系得:
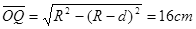 (1分)
(1分)

故金箔cd被α粒子射中区域的长度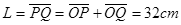 (1分)
(1分)
(3)设从Q点穿出的α粒子的速度为v′,因半径O2Q∥场强E,则v′⊥E,故穿出的α粒子在电场中做类平抛运动,轨迹如图所示。
沿速度v′方向做匀速直线运动, 位移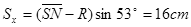 (1分)
(1分)
沿场强E方向做匀加速直线运动,位移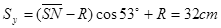 (1分)
(1分)
则由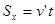
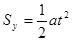
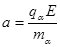 得:
得:
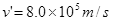 (2分)
(2分)
故此α粒子从金箔上穿出时,损失的动能为
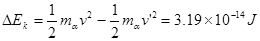 (2分)
(2分)
考点:本题考查带电粒子在磁场中的运动、动能定理。

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案 如图所示,半径为r、圆心为O1的虚线所围的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有一竖直放置的平行金属板M和N,两板间距离为L,在MN板中央各有一个小孔O2、O3、O1、O2、O3在同一水平直线上,与平行金属板相接的是两条竖直放置间距为L的足够长的光滑金属导轨,导体棒PQ与导轨接触良好,与阻值为R的电阴形成闭合回路(导轨与导体棒的电阻不计),该回路处在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,整个装置处在真空室中,有一束电荷量为+q、质量为m的粒子流(重力不计),以速率v0从圆形磁场边界上的最低点E沿半径方向射入圆形磁场区域,最后从小孔O3射出.现释放导体棒PQ,其下滑h后开始匀速运动,此后粒子恰好不能从O3射出,而从圆形磁场的最高点F射出.求:
如图所示,半径为r、圆心为O1的虚线所围的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有一竖直放置的平行金属板M和N,两板间距离为L,在MN板中央各有一个小孔O2、O3、O1、O2、O3在同一水平直线上,与平行金属板相接的是两条竖直放置间距为L的足够长的光滑金属导轨,导体棒PQ与导轨接触良好,与阻值为R的电阴形成闭合回路(导轨与导体棒的电阻不计),该回路处在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,整个装置处在真空室中,有一束电荷量为+q、质量为m的粒子流(重力不计),以速率v0从圆形磁场边界上的最低点E沿半径方向射入圆形磁场区域,最后从小孔O3射出.现释放导体棒PQ,其下滑h后开始匀速运动,此后粒子恰好不能从O3射出,而从圆形磁场的最高点F射出.求: (2011?自贡模拟)如图所示,半径为r圆心为0的虚线所围的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有一竖直放置的平行金属板M和N,两板间距离为在MN板中央各有一个小孔02、O3,O1,O2,O3在同一水平直线上,与平行金属板相接的是两条竖直放置间距为L的足够长的光滑金属导轨,导体棒PQ与导轨接触良好,与阻值为R的电阻形成闭合回路.(导轨与导体棒的电阻不计),该回路处在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,整个装置处在真空室中,有一束电荷量为+q、质量为m的粒子流(重力不计),以速率V0从圆形磁场边界上的最低点E沿半径方向射入圆形磁场区域,最后从小孔O3射出.现释放导体棒PQ,其下滑h后开始匀速运动,此后粒子恰好不能从O3射出,而是从圆形磁场的最高点F射出.求:
(2011?自贡模拟)如图所示,半径为r圆心为0的虚线所围的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有一竖直放置的平行金属板M和N,两板间距离为在MN板中央各有一个小孔02、O3,O1,O2,O3在同一水平直线上,与平行金属板相接的是两条竖直放置间距为L的足够长的光滑金属导轨,导体棒PQ与导轨接触良好,与阻值为R的电阻形成闭合回路.(导轨与导体棒的电阻不计),该回路处在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,整个装置处在真空室中,有一束电荷量为+q、质量为m的粒子流(重力不计),以速率V0从圆形磁场边界上的最低点E沿半径方向射入圆形磁场区域,最后从小孔O3射出.现释放导体棒PQ,其下滑h后开始匀速运动,此后粒子恰好不能从O3射出,而是从圆形磁场的最高点F射出.求:
