题目内容
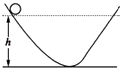
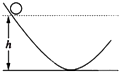
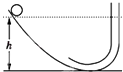
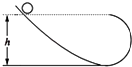
【题目】质量均为m的物体A和B分别系在一根不计质量的细绳两端,绳子跨过固定在倾角为30°的光滑斜面顶端的定滑轮上,斜面固定在水平地面上.开始时把物体B拉到斜面底端,这时物体A离地面的高度为0.8m,如图所示.若摩擦力均不计,从静止开始放手让它们运动,取g=10m/s2 . 求:
(1)物体A着地时的速度
(2)物体A着地后物体B沿斜面上滑的最大距离.
【答案】
(1)
解:物体A着地时速度大小为v,
运动过程中AB系统机械能守恒: ![]()
h=0.8m
得v=2(m/s)
(2)
解:A着地后,物体B沿斜面上滑的最大距离为L, ![]()
得L=0.4(m)
【解析】A、B开始运动到A着地过程中,分析系统的受力及做功情况,系统的机械能守恒,运用机械能守恒定律求出它们的速度.
A着地后,B沿斜面做匀减速运动,当速度减为零时,B能沿斜面滑行的距离最大.
【考点精析】利用机械能守恒及其条件对题目进行判断即可得到答案,需要熟知在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变.

【题目】用发光二极管制成的LED灯具有发光效率高、使用寿命长等优点,在生产与生活中得到广泛应用.某同学找到一个LED灯泡,测得它两端电压U和通过的电流I的数据如下表:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
U/V | 0.00 | … | … | … | 2.60 | 2.72 | 2.80 | 2.92 | 3.00 | 3.17 | 3.30 | 3.50 |
I/mA | 0.00 | … | … | … | 1.29 | 5.77 | 8.71 | 19.05 | 27.30 | 38.86 | 50.63 | 68.00 |
(1)实验室提供的器材如下:
A.电流表(量程0~0.6A,内阻约1Ω)
B.电流表(量程0~100mA,内阻约50Ω)
C.电压表(量程0~6V,内阻约50kΩ)
D.电压表(量程0~15V,内阻约60kΩ)
E.电源(电动势6V,内阻不计)
F.滑动变阻器(阻值范围0~10Ω,允许最大电流3A)
G.开关,导线
该同学做实验时,电压表选用的是 , 电流表选用的是;(填选项前字母)
(2)请在图中以笔画线代替导线,按实验要求将实物图中的连线补充完整;
(3)开关闭合之前,图中滑动变阻器的滑片应该置于(填“A端”、“B端”或“A、B正中间”);
(4)若该LED灯泡的额定电压为3V,则此LED灯泡的额定功率为 .