题目内容
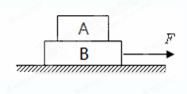
有一质量为m的木块,从半径为r的圆弧曲面上的a点滑向b点,如图所示.如果由于摩擦使木块的运动速率保持不变,则以下叙述正确的是 ( )
| A.木块的加速度不变 |
| B.木块所受的合外力为零 |
| C.木块所受的力都不对其做功 |
| D.木块所受的合外力不为零,但合外力对木块所做的功为零 |
D
解析试题分析:木块沿曲面运动,速率不变,加速度的方向变了,所以A错;木块做曲线运动,合力不为0,所以B错;重力和摩擦力都对木块做了功,所以C错,木块速率不变,由动能定理可知,合外力对木块做功为0,所以D正确。
考点:动能定理,牛顿第二定律,向心力公式

如图所示,在半径为R的四分之一光滑圆弧轨道的顶端a点,质量为m的物块(可视为质点)由静止开始下滑,经圆弧最低点b滑上粗糙水平面,圆弧轨道在b点与水平轨道平滑相接,物块最终滑至c点停止。若物块与水平面问的动摩擦因数为μ,下列说法正确的是( ) 
A.物块滑到b点时的速度为 |
| B.物块滑到b点时对b点的压力是2mg |
C.c点与b点的距离为 |
| D.整个过程中物块机械能损失了mgR |
如图所示,半径r=0.8m的光滑圆轨道被竖直固定在水平地面上,圆轨道最低处有一质量为0. 4kg的小球(小球的半径比r小很多)。现给小球一个水平向右的初速度v0,下列关于在小球的运动过程中说法正确的是(g取10m/s2)( )
| A.v0≤4m/s可以使小球不脱离轨道 |
B.v0≥4 m/s可以使小球不脱离轨道 m/s可以使小球不脱离轨道 |
| C.设小球能在圆轨道中做完整的圆周运动,在最低点与最高点对轨道的压力之差为24N |
| D.设小球能在圆轨道中做完整的圆周运动,在最低点与最高点对轨道的压力之差为20N |
如图所示,小球用两根轻质橡皮条悬吊着,且AO呈水平状态,BO跟竖直方向的夹角为α,那么在剪断某一根橡皮条的瞬间,小球的加速度情况是 
| A.剪断AO瞬间,小球加速度大小是零 |
| B.剪断AO瞬间,小球加速度大小a=gtanα |
| C.剪断BO瞬间,小球加速度大小是零 |
| D.剪断BO瞬间,小球加速度大小a=gcosα |
物理学中有些问题的结论不一定必须通过计算才能验证,有时只需要通过一定的分析就可以判断结论是否正确。如图所示,倾角为θ的足够长的粗糙斜面固定在水平地面上,质量为M的木块上固定一轻直角支架,在支架末端用轻绳悬挂一质量为m的小球。由静止释放木块,木块沿斜面下滑,稳定后轻绳与竖直方向夹角为α,则木块与斜面间的动摩擦因数为 ( ) 
| A.μ=tanθ | B.μ= tanα |
| C.μ= tan(θ-α) | D.μ= tan(θ+α) |
压敏电阻的阻值会随所受压力的增大而减小,某同学利用压敏电阻的这种特性设计了一个探究电梯运动情况的装置,该装置的示意图如图所示,将压敏电阻平放在电梯内,其受压面向上,在受力面上放一物体m,电梯静止时电流表示数为I0,当电梯做四种不同的运动时,电流表示数分别如图甲、乙、丙和丁所示,下列判断中正确的是( )
| A.甲图表示电梯可能在做匀速运动 |
| B.乙图表示电梯可能向上做匀加速运动 |
| C.丙图表示电梯可能向上做匀加速运动 |
| D.丁图表示电梯可能向下做匀减速运动 |
如图所示,螺旋形光滑轨道竖直放置,P、Q为对应的轨道最高点,一个小球以一定速度沿轨道切线方向进入轨道,且能过轨道最高点P,则下列说法中不正确的是 ( ).
| A.轨道对小球做正功,小球的线速度vP>vQ |
| B.轨道对小球不做功,小球的角速度ωP<ωQ |
| C.小球的向心加速度aP>aQ |
| D.轨道对小球的压力FP>FQ |