题目内容
如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的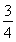 圆弧轨道,两轨道相切于B点.在外力作用下,一小球从A点由静止开始做匀加速直线运动,到达B点时撤除外力.已知小球刚好能沿圆轨道经过最高点C,重力加速度大小为g.求:
圆弧轨道,两轨道相切于B点.在外力作用下,一小球从A点由静止开始做匀加速直线运动,到达B点时撤除外力.已知小球刚好能沿圆轨道经过最高点C,重力加速度大小为g.求:
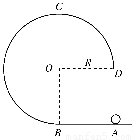
(1)小球在AB段运动的加速度的大小;
(2)小球从D点运动到A点所用的时间.
【答案】
(1)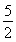 g (2)(
g (2)(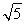 -
-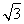 )
) 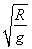
【解析】(1)小球在BCD段运动时,受到重力mg、轨道正压力FN的作用,如图所示.据题意,FN≥0,且小球在最高点C所受轨道正压力为零,即FNC=0????????????? ①
设小球在C点的速度大小为vC,根据牛顿第二定律有
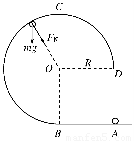
mg=m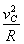 ????????????? ????????????? ②
????????????? ????????????? ②
小球从B点运动到C点机械能守恒.设B点处小球的速度大小为vB,有
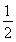 mv
mv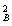 =
=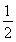 mv
mv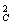 +2mgR????????????? ????????????? ③
+2mgR????????????? ????????????? ③
由于小球在AB段由静止开始做匀加速运动,设加速度大小为a,由运动学公式有
v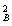 =2aR????????????? ????????????? ④
=2aR????????????? ????????????? ④
联立②③④得a=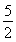 g????????????? ????????????? ⑤
g????????????? ????????????? ⑤
(2)设小球在D处的速度大小为vD,下落到A点时的速度大小大小为v,由机械能守恒有
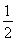 mv
mv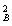 =
=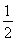 mv
mv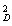 +mgR????????????? ????????????? ⑥
+mgR????????????? ????????????? ⑥
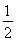 mv
mv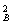 =
=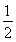 mv2????????????? ????????????? ⑦
mv2????????????? ????????????? ⑦
设从D点运动到A点所用的时间为t,由运动学公式得
gt=v-vD????????????? ????????????? ⑧
联立④⑤⑥⑦⑧解得t=(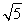 -
-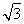 )
)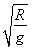 .
.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的3/4圆弧轨道,两轨道相切与B点.在外力作用下,一小球从A点由静止开始做匀加速直线运动,到达B点时撤除外力.已知小球刚好能沿圆轨道经过最高点C,重力加速度大小为g.求:
如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的3/4圆弧轨道,两轨道相切与B点.在外力作用下,一小球从A点由静止开始做匀加速直线运动,到达B点时撤除外力.已知小球刚好能沿圆轨道经过最高点C,重力加速度大小为g.求: (2012?海南)如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的
(2012?海南)如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的 如图,在竖直平面内有一固定光滑轨道,其中AB部分是倾角为37°的直轨道,BCD部分是以O为圆心、半径为R的圆弧轨道,两轨道相切于B点,D点与O点等高,A点在D点的正下方.质量为m的小球在沿斜面向上的拉力F作用下,从A点由静止开始做变加速直线运动,到达B点时撤去外力.已知小球刚好能沿圆轨道经过最高点C,然后经过D点落回到A点.已知sin37°=0.6,cos37°=0.8,重力加速度大小为g.求
如图,在竖直平面内有一固定光滑轨道,其中AB部分是倾角为37°的直轨道,BCD部分是以O为圆心、半径为R的圆弧轨道,两轨道相切于B点,D点与O点等高,A点在D点的正下方.质量为m的小球在沿斜面向上的拉力F作用下,从A点由静止开始做变加速直线运动,到达B点时撤去外力.已知小球刚好能沿圆轨道经过最高点C,然后经过D点落回到A点.已知sin37°=0.6,cos37°=0.8,重力加速度大小为g.求 如图,在竖直平面内有一匀强电场,一带电量为+q、质量为m的小球在力F的作用下沿图中虚线由A至B做竖直向上的匀速运动.已知力F和AB间夹角为θ,AB间距离为d,重力加速度为g.则电场强度E的最小值为
如图,在竖直平面内有一匀强电场,一带电量为+q、质量为m的小球在力F的作用下沿图中虚线由A至B做竖直向上的匀速运动.已知力F和AB间夹角为θ,AB间距离为d,重力加速度为g.则电场强度E的最小值为 如图,在竖直平面内有一“v”形槽,其底部BC是一段圆弧,两侧都与光滑斜槽分别相切,相切处B、C位于同一水平面上.一小物体从右侧斜槽上距BC平面高度为2h的A处由静止开始下滑,经圆弧槽再滑上左侧斜槽,最高能到达距BC面高度为h的D点,接着小物体再向下滑回,若不考虑空气阻力,则( )
如图,在竖直平面内有一“v”形槽,其底部BC是一段圆弧,两侧都与光滑斜槽分别相切,相切处B、C位于同一水平面上.一小物体从右侧斜槽上距BC平面高度为2h的A处由静止开始下滑,经圆弧槽再滑上左侧斜槽,最高能到达距BC面高度为h的D点,接着小物体再向下滑回,若不考虑空气阻力,则( )