题目内容
 (2012?海南)如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的
(2012?海南)如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的| 3 | 4 |
(1)小球从在AB段运动的加速度的大小;
(2)小球从D点运动到A点所用的时间.
分析:(1)物体恰好通过最高点,意味着在最高点是轨道对滑块的压力为0,即重力恰好提供向心力,这样我们可以求出C点速度,从B到C的过程中运用动能定理求出B点速度,根据匀加速直线运动位移速度公式即可求解加速度;
(2)小球离开D点做加速度为D的匀加速直线运动,根据位移时间公式即可求解时间.
(2)小球离开D点做加速度为D的匀加速直线运动,根据位移时间公式即可求解时间.
解答:解:(1)小滑块恰好通过最高点,则有:mg=m
解得:vC=
从B到C的过程中运用动能定理得:
mvC2-
mvB2=-mg?2R
解得:vB=
根据位移速度公式得:2aR=vB2
解得:a=
g
(2)从C到D的过程中运用动能定理得:
mvD2-
mvC2=mgR
解得:vD=
小球离开D点做加速度为D的匀加速直线运动,根据位移时间公式得:
R=vDt+
gt2
解得:t=(
-
)
答:(1)小球从在AB段运动的加速度的大小为
g;
(2)小球从D点运动到A点所用的时间为(
-
)
.
| vC2 |
| R |
解得:vC=
| gR |
从B到C的过程中运用动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:vB=
| 5gR |
根据位移速度公式得:2aR=vB2
解得:a=
| 5 |
| 2 |
(2)从C到D的过程中运用动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:vD=
| 3gR |
小球离开D点做加速度为D的匀加速直线运动,根据位移时间公式得:
R=vDt+
| 1 |
| 2 |
解得:t=(
| 5 |
| 3 |
|
答:(1)小球从在AB段运动的加速度的大小为
| 5 |
| 2 |
(2)小球从D点运动到A点所用的时间为(
| 5 |
| 3 |
|
点评:本题主要考查了动能定理,运动学基本公式的直接应用,物体恰好通过C点是本题的突破口,这一点要注意把握,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012?海南)如图,表面处处同样粗糙的楔形木块abc固定在水平地面上,ab面和bc面与地面的夹角分别为α和β,且α>β.一初速度为v0的小物块沿斜面ab向上运动,经时间t0后到达顶点b时,速度刚好为零;然后让小物块立即从静止开始沿斜面bc下滑.在小物块从a运动到c的过程中,可能正确描述其速度大小v与时间t的关系的图象是( )
(2012?海南)如图,表面处处同样粗糙的楔形木块abc固定在水平地面上,ab面和bc面与地面的夹角分别为α和β,且α>β.一初速度为v0的小物块沿斜面ab向上运动,经时间t0后到达顶点b时,速度刚好为零;然后让小物块立即从静止开始沿斜面bc下滑.在小物块从a运动到c的过程中,可能正确描述其速度大小v与时间t的关系的图象是( )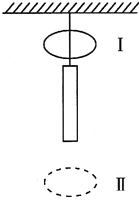 (2012?海南)如图,一质量为m的条形磁铁用细线悬挂在天花板上,细线从一水平金属圆环中穿过.现将环从位置Ⅰ释放,环经过磁铁到达位置Ⅱ.设环经过磁铁上端和下端附近时细线的张力分别为T1和T2,重力加速度大小为g,则( )
(2012?海南)如图,一质量为m的条形磁铁用细线悬挂在天花板上,细线从一水平金属圆环中穿过.现将环从位置Ⅰ释放,环经过磁铁到达位置Ⅱ.设环经过磁铁上端和下端附近时细线的张力分别为T1和T2,重力加速度大小为g,则( ) (2012?海南)如图,直线上有O、a、b、c四点,ab间的距离与bc间的距离相等.在O点处有固定点电荷.已知b点电势高于c点电势.若一带负电荷的粒子仅在电场力作用下先从c点运动到b点,再从b点运动到a点,则( )
(2012?海南)如图,直线上有O、a、b、c四点,ab间的距离与bc间的距离相等.在O点处有固定点电荷.已知b点电势高于c点电势.若一带负电荷的粒子仅在电场力作用下先从c点运动到b点,再从b点运动到a点,则( ) (2012?海南)N(N>1)个电荷量均为q(q>0)的小球,均匀分布在半径为R的圆周上,示意如图.右移去位于圆周上P点的一个小球,则圆心O点处的电场强度大小为
(2012?海南)N(N>1)个电荷量均为q(q>0)的小球,均匀分布在半径为R的圆周上,示意如图.右移去位于圆周上P点的一个小球,则圆心O点处的电场强度大小为