题目内容
12.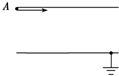 如图所示,两带电平行金属板水平正对放置,下极板接地,极板长L=2cm,极板宽d=1cm,一质量为m、所带电荷量为q的带正电粒子从上极板的边缘A以初动能Ek水平向右射入电场,刚好从下极板的右边缘射出,粒子重力不计,则下列说法正确的是( )
如图所示,两带电平行金属板水平正对放置,下极板接地,极板长L=2cm,极板宽d=1cm,一质量为m、所带电荷量为q的带正电粒子从上极板的边缘A以初动能Ek水平向右射入电场,刚好从下极板的右边缘射出,粒子重力不计,则下列说法正确的是( )| A. | 该粒子在入射点A时的电势能为Ek | |
| B. | 该粒子到达下极板右边缘时的速度与水平方向成30°角 | |
| C. | 该粒子到达下极板右边缘时的动能为2Ek | |
| D. | 该粒子通过两极板中间位置时的动能为0.5Ek |
分析 带电粒子进入电场后做类平抛运动,由分速度公式分析粒子到达下极板右边缘时的速度与水平方向的夹角.由末速度与初速度的关系求末动能.粒子通过两极板中间位置时求出竖直分速度,即可求得动能.根据能量守恒定律研究电势能.
解答 解:设带电粒子在A点的初速度为v0.到达下极板右边缘时的速度为v,动能为Ek′.
则得:v=$\sqrt{2}$v0,
由题有:Ek=$\frac{1}{2}$mv02,Ek′=$\frac{1}{2}$mv2
则得:Ek′=2Ek
设粒子到达下极板右边缘时的速度与水平方向成α角.则有:tanα=$\frac{{v}_{y}}{{v}_{0}}$
据题粒子到达下极板右边缘时竖直分位移与水平分位移之比为:$\frac{d}{L}$=$\frac{\frac{{v}_{Y}}{2}t}{{v}_{0}t}$=$\frac{{v}_{y}}{2{v}_{0}}$
联立解得:tanα=$\frac{2d}{L}$=$\frac{2×1}{2}$=1,则得:α=45°,故B错误;
设带电粒子在A点的初速度为v0.到达下极板右边缘时的速度为v,动能为Ek′.
则得:v=$\sqrt{2}$v0
由题有:Ek=$\frac{1}{2}$mv02,Ek′=$\frac{1}{2}$mv2
则得:Ek′=2Ek.故C正确.
粒子在竖直方向做匀加速直线运动,由v2=2ay得:该粒子通过两极板中间位置时竖直分速度为下极板右边缘时竖直分速度的$\frac{\sqrt{2}}{2}$v0倍,即为$\frac{\sqrt{2}}{2}{v}_{0}$,故粒子通过两极板中间位置时的动能为:Ek′=$\frac{1}{2}$m(vx2+vy2)=1.5Ek.故D错误;
由上分析知,带电粒子从A到下极板右边缘时动能增加Ek,由能量守恒知电势能减少Ek,因此该粒子在入射点A时的电势能为Ek.故A正确.
故选:AC.
点评 本题考查了粒子在匀强电场中的运动,要知道带电粒子在匀强电场中做类平抛运动,研究的方法与平抛运动类似:运动的合成与分解,应用匀速运动规律、牛顿第二定律、匀变速运动规律即可正确解题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案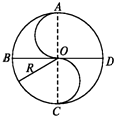 一人晨练,按图所示走半径为R的中国古代八卦图,中央S部分是两个直径为R的半圆,BD、CA分别为西东、南北指向.他从A点出发沿曲线ABCOADC行进,则当他到D点时,他的路程和位移大小及位移的方向分别为( )
一人晨练,按图所示走半径为R的中国古代八卦图,中央S部分是两个直径为R的半圆,BD、CA分别为西东、南北指向.他从A点出发沿曲线ABCOADC行进,则当他到D点时,他的路程和位移大小及位移的方向分别为( )| A. | 2πR R 向西南 | B. | 2.5πR $\sqrt{2}$R 向东南 | C. | πR R 向东南 | D. | 3πR R 向西北 |
| A. | 物体的重力势能增加了2mgh | B. | 物体的动能增加了2mgh | ||
| C. | 物体的机械能保持不变 | D. | 物体的机械能增加了3mgh |
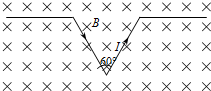 长为4L的直导线等分成四等份,拆成如图所示的图形,其中的V形导线夹角为60°,整个图形置于与其所在平面相垂直的匀强磁场中,磁场的磁感应强度为B,当在该导线中通以大小为I的电流时,该V形通电导线受到的安培力大小为( )
长为4L的直导线等分成四等份,拆成如图所示的图形,其中的V形导线夹角为60°,整个图形置于与其所在平面相垂直的匀强磁场中,磁场的磁感应强度为B,当在该导线中通以大小为I的电流时,该V形通电导线受到的安培力大小为( )| A. | BIL | B. | 2BIL | C. | 3BIL | D. | 4BIL |
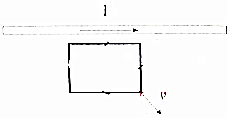 如图所示.光滑绝缘无限大水平面上固定一通电长直导线.质量为0.02kg的正方形金属框在该水平面内以2m/s、与电流方向成60°角的速度滑出.下列说法中正确的是( )
如图所示.光滑绝缘无限大水平面上固定一通电长直导线.质量为0.02kg的正方形金属框在该水平面内以2m/s、与电流方向成60°角的速度滑出.下列说法中正确的是( )| A. | 金属框中无电流,一直做匀速直线运动 | |
| B. | 金属框最终在水平面上做匀速直线运动 | |
| C. | 金属框最终将静止在水平面上的某处 | |
| D. | 金属框中产生的热量最多为0.04J |
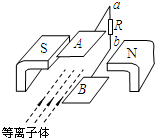 目前世界上正在研究的一种新型发电机叫磁流体发电机,图11表示它的发电原理:将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体上来说呈电中性)喷入磁场,由于等离子体在磁场力的作用下运动方向发生偏转,磁场中的两块金属板A和B上就会聚集电荷,从而在两板间产生电压.在图示磁极配置的情况下,金属板的电势高低和通过电阻R的电流方向分别是( )
目前世界上正在研究的一种新型发电机叫磁流体发电机,图11表示它的发电原理:将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体上来说呈电中性)喷入磁场,由于等离子体在磁场力的作用下运动方向发生偏转,磁场中的两块金属板A和B上就会聚集电荷,从而在两板间产生电压.在图示磁极配置的情况下,金属板的电势高低和通过电阻R的电流方向分别是( )| A. | A板电势高,电流方向a→b | B. | A板电势高,电流方向b→a | ||
| C. | B板电势高,电流方向a→b | D. | B板电势高,电流方向b→a |
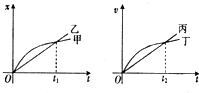
| A. | 甲车做直线运动,乙车做曲线运动 | |
| B. | 0~t2时间内,丙、丁两车的平均速度相等 | |
| C. | 0~t2时间内,丙、丁两车在t2时刻相距最远 | |
| D. | 0~t1时间内,甲车通过的路程大于乙车通过的路程 |
 如图所示,光滑小球静止在两个平面间,一个面恰水平,一个面倾斜,则小球受到的作用力有2个,它们分别是重力和水平面的支持力.
如图所示,光滑小球静止在两个平面间,一个面恰水平,一个面倾斜,则小球受到的作用力有2个,它们分别是重力和水平面的支持力.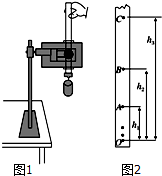 利用如图所示的装置验证机械能守恒定律.
利用如图所示的装置验证机械能守恒定律.