题目内容
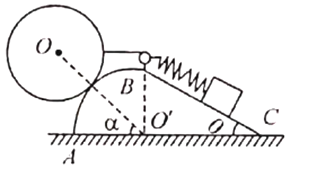
【题目】如图所示，半径为R的光滑圆弧轨道ABC固定在竖直平面内，O为圆心，OC竖直，OA水平，B为圆弧的最低点，B点紧靠一足够长的平台MN。D点位于A点正上方。现从D点无初速度释放一个可视为质点的小球，在A点进人圆弧轨道，从C点飞出后做平抛运动，不计空气阻力，重力加速度为g，求:
(1)通过计算说明小球能否重新落回到轨道内侧;
(2)若DA之间的高度差为3R，求小球落地点P到B点的距离L。
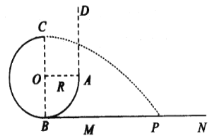
【答案】(1)小球不能重新落回到轨道内侧 (2)L=4R
【解析】
(1)设小球在C点的最小速度为v0，由牛顿第二定律
设小球下降高度R所用时间为t1。
在时间t1内的水平位移为
，解得
所以小球不能重新落回到轨道内侧。
(2)设小球到达C点的速度人小为vc，对小球从D点到C点的过程。
由动能定理
小球从C点飞出后做平抛运动，设经过时间以落到P点。竖直方向
水平方向
解得
L=4R
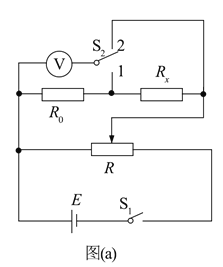
【题目】一课外实验小组用如图所示的电路测量某待测电阻Rx的阻值，图中R0为标准定值电阻（R0=20.0 Ω）；
可视为理想电压表．S1为单刀开关，S2位单刀双掷开关，E为电源，R为滑动变阻器．采用如下步骤完成实验：
（1）按照实验原理线路图（a），将图（b）中实物连线_____________；
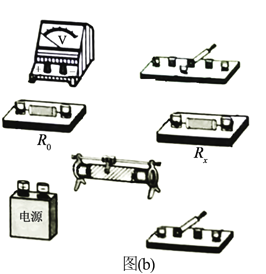
（2）将滑动变阻器滑动端置于适当位置，闭合S1；
（3）将开关S2掷于1端，改变滑动变阻器动端的位置，记下此时电压表的示数U1；然后将S2掷于2端，记下此时电压表的示数U2；
（4）待测电阻阻值的表达式Rx=_____________（用R0、U1、U2表示）；
（5）重复步骤（3），得到如下数据：
1 | 2 | 3 | 4 | 5 | |
U1/V | 0.25 | 0.30 | 0.36 | 0.40 | 0.44 |
U2/V | 0.86 | 1.03 | 1.22 | 1.36 | 1.49 |
| 3.44 | 3.43 | 3.39 | 3.40 | 3.39 |
（6）利用上述5次测量所得
的平均值，求得Rx=__________Ω．（保留1位小数）