题目内容
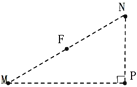
【题目】如图所示,静止于A处的离子,经电压为U的加速电场加速后沿图中的半圆弧虚线通过静电分析器,从P点垂直CN进入矩形区域的有界匀强电场,电场方向水平向左。静电分析器通道内有均匀辐向分布的电场,已知圆弧所在处场强大小都为E0,方向沿圆弧半径指向圆心O。离子质量为m、电荷量为q,QN=2d、PN=3d,离子重力不计。

(1)离子离开加速电场时的速度;
(2)求圆弧虚线对应的半径R的大小;
(3)若离子恰好能打在QN的中点上,求矩形区域QNCD内匀强电场场强E的值
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)(2)离子在加速电场中加速时,电场力做功,动能增加,根据动能定理列出方程;粒子进入静电分析器,靠电场力提供向心力,结合牛顿第二定律列出方程,即可求出圆弧虚线对应的半径R的大小;
(3)离子进入矩形区域的有界匀强电场后做类平抛运动,将其进行正交分解,由牛顿第二定律和运动学公式结合,可求解场强E0的值。
(1) 离子在加速电场中加速,根据动能定理,有:
![]()
解得:![]() ;
;
(2) 离子在辐向电场中做匀速圆周运动,电场力提供向心力,根据牛顿第二定律,有:
![]()
解得:![]() ;
;
(3) 离子做类平抛运动,有:
d=vt
![]()
由牛顿第二定律得:
qE=ma,得![]() 。
。

练习册系列答案
相关题目