题目内容
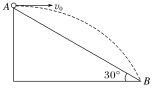
【题目】如图所示，AB为固定斜面，倾角为30°，小球从A点以初速度v0水平抛出，恰好落到斜面上的B点（空气阻力不计，重力加速度为g）。求：
(1)求小球在空中飞行的时间；
(2)求小球与斜面间的最大距离；
(3)在最大距离处将AB抛物线一分为二，求小球沿斜面方向的位移差是多少。
【答案】(1)
；(2)
；(3)
【解析】
(1)设飞行时间为t，则水平方向位移
lABcos 30°＝v0t
竖直方向位移
lABsin 30°＝
gt2
解得
t＝
tan 30°＝
(2) 当小球运动方向与斜面平行时，小球离斜面最远，此时
，
当
时，小球离斜面最远．则最远距离为
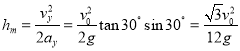
(3)根据以上分析可知，斜面高
斜面长
从抛出到离斜面最远，水平位移
，竖直位移
，根据几何关系可知，沿斜面方向位移
则从离斜面最远到底端，沿斜面方向位移
则小球沿斜面方向的位移差
练习册系列答案
计算高手系列答案
相关题目
